
【题目】某公司在某市五个区投放共享单车供市民使用,投放量的分布及投放后的使用情况统计如下.
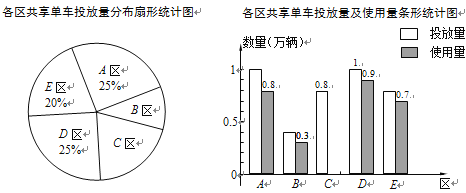
(1)该公司在全市一共投放了 万辆共享单车;
(2)在扇形统计图中,B区所对应扇形的圆心角为 °;
(3)该公司在全市投放的共享单车的使用量占投放量的85%,请计算C区共享单车的使用量并补全条形统计图.
科目:初中数学 来源: 题型:
【题目】为了传承优秀传统文化,某校开展“经典诵读”比赛活动,诵读材料有《论语》,《三字经》,《弟子规》(分别用字母A,B,C依次表示这三个诵读材料),将A,B,C这三个字母分别写在3张完全相同的不透明卡片的正面上,把这3张卡片背面朝上洗匀后放在桌面上.小明和小亮参加诵读比赛,比赛时小明先从中随机抽取一张卡片,记录下卡片上的内容,放回后洗匀,再由小亮从中随机抽取一张卡片,选手按各自抽取的卡片上的内容进行诵读比赛.
(1)小明诵读《论语》的概率是;
(2)请用列表法或画树状图(树形图)法求小明和小亮诵读两个不同材料的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABO的顶点O在坐标原点,点B在x轴上,∠ABO=90°,∠AOB=30°,OB=2 ![]() ,反比例函数y=
,反比例函数y= ![]() (x>0)的图象经过OA的中点C,交AB于点D.
(x>0)的图象经过OA的中点C,交AB于点D. 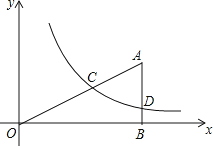
(1)求反比例函数的关系式;
(2)连接CD,求四边形CDBO的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(题文)图1是一个长为2a,宽为2b的长方形,沿图中虚线剪开分成四块小长方形,然后按图2的形状拼成一个正方形.


![]() 图2的阴影部分的正方形的边长是______.
图2的阴影部分的正方形的边长是______.
![]() 用两种不同的方法求图中阴影部分的面积.
用两种不同的方法求图中阴影部分的面积.
(方法1)![]() = ____________;
= ____________;
(方法2)![]() = ____________;
= ____________;
(3) 观察图2,写出(a+b)2,(a-b)2,ab这三个代数式之间的等量关系;
![]() 根据
根据![]() 题中的等量关系,解决问题:若m+n=10,m-n=6,求mn的值.
题中的等量关系,解决问题:若m+n=10,m-n=6,求mn的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年5月,某大型商业集团随机抽取所属的m家商业连锁店进行评估,将各连锁店按照评估成绩分成了A、B、C、D四个等级,绘制了如图尚不完整的统计图表.
评估成绩n(分) | 评定等级 | 频数 |
90≤n≤100 | A | 2 |
80≤n<90 | B | |
70≤n<80 | C | 15 |
n<70 | D | 6 |
根据以上信息解答下列问题:
(1)求m的值;
(2)在扇形统计图中,求B等级所在扇形的圆心角的大小;(结果用度、分、秒表示)
(3)从评估成绩不少于80分的连锁店中任选2家介绍营销经验,求其中至少有一家是A等级的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:
如图①,在平面直角坐标系中,若已知点A(xA,yA)和点C(xC,yC),点M为线段AC的中点,利用三角形全等的知识,有△AMP≌△CMQ,则有PM=MQ,PA=QC,即xM﹣xA=xC﹣xM,yA﹣yM=yM﹣yC,从而有 ,即中点M的坐标为(
,即中点M的坐标为(![]() ,
,![]() ).
).

基本知识:
(1)如图①,若A、C点的坐标分别A(﹣1,3)、C(3,﹣1),求AC中点M的坐标;
方法提炼:
(2)如图②,在平面直角坐标系中,ABCD的顶点A、B、C的坐标分别为(﹣1,5)、(﹣2,2)、(3,3),求点D的坐标;
(3)如图③,点A是反比例函数y=![]() (x>0)上的动点,过点A作AB∥x轴,AC∥y轴,分别交函数y═
(x>0)上的动点,过点A作AB∥x轴,AC∥y轴,分别交函数y═![]() (x>0)的图象于点B、C,点D是直线y=2x上的动点,请探索在点A运动过程中,以A、B、C、D为顶点的四边形能否为平行四边形,若能,求出此时点A的坐标;若不能,请说明理由.
(x>0)的图象于点B、C,点D是直线y=2x上的动点,请探索在点A运动过程中,以A、B、C、D为顶点的四边形能否为平行四边形,若能,求出此时点A的坐标;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,内部有6个全等的正方形,小正方形的顶点E、F、G、H分
别在边AD、AB、BC、CD上,则tan∠DEH=( )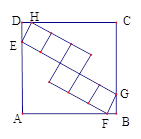
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在长方形ABCD中,AB=3,BC=4,动点P从点A开始按A→B→C→D的方向运动到点D.如图,设动点P所经过的路程为x,△APD的面积为y.(当点P与点A或D重合时,y=0)
(1)写出y与x之间的函数解析式;
(2)画出此函数的图象.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了改善办学条件,计划购置一批电子白板和一批笔记本电脑,经投标,购买1块电子白板比买3台笔记本电脑多3000元,购买4块电子白板和5台笔记本电脑共需80000元.
(1)求购买1块电子白板和一台笔记本电脑各需多少元?
(2)根据该校实际情况,需购买电子白板和笔记本电脑的总数为396,要求购买的总费用不超过2700000元,并购买笔记本电脑的台数不超过购买电子白板数量的3倍,该校有哪几种购买方案?
(3)上面的哪种购买方案最省钱?按最省钱方案购买需要多少钱?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com