
����Ŀ��ijѧУΪ�˸��ư�ѧ�������ƻ�����һ�����Ӱװ��һ���ʼDZ����ԣ���Ͷ�꣬����1����Ӱװ����3̨�ʼDZ����Զ�3000Ԫ������4����Ӱװ��5̨�ʼDZ����Թ���80000Ԫ��
��1������1����Ӱװ��һ̨�ʼDZ����Ը������Ԫ��
��2�����ݸ�Уʵ��������蹺����Ӱװ�ͱʼDZ����Ե�����Ϊ396��Ҫ������ܷ��ò�����2700000Ԫ��������ʼDZ����Ե�̨��������������Ӱװ�������3������У���ļ��ֹ�����
��3����������ֹ�����ʡǮ������ʡǮ����������Ҫ����Ǯ��
���𰸡���1������1����Ӱװ���Ҫ15000Ԫ��һ̨�ʼDZ�������Ҫ4000Ԫ��2�������ֹ���������һ������ʼDZ�����295̨��������Ӱװ�101�飻������������ʼDZ�����296̨��������Ӱװ�100�飻������������ʼDZ�����297̨��������Ӱװ�99�顣��3��������ʼDZ�����297̨��������Ӱװ�99��ʱ����ʡǮ���������2673000Ԫ
���������⣺��1���蹺��1����Ӱװ���ҪxԪ��һ̨�ʼDZ�������ҪyԪ��������ã�
![]() ����ã�
����ã�![]() ��
��
�𣺹���1����Ӱװ���Ҫ15000Ԫ��һ̨�ʼDZ�������Ҫ4000Ԫ��
��2���蹺������Ӱװ�a�飬����ʼDZ����ԣ�396��a��̨��������ã�
![]() ����ã�
����ã�![]() ��
��
��a��������a=99��100��101�������������297��296��295��
����У�����ֹ�����
����һ������ʼDZ�����295̨��������Ӱװ�101�飻
������������ʼDZ�����296̨��������Ӱװ�100�飻
������������ʼDZ�����297̨��������Ӱװ�99�顣
��3���蹺��ʼDZ�������Ϊz̨������ʼDZ����Ժ͵��Ӱװ���ܷ���ΪWԪ��
��W=4000z+15000��396��z��=��11000z+5940000��
��W��z���������С������z=297ʱ��W����Сֵ=2673000��Ԫ��
��������ʼDZ�����297̨��������Ӱװ�99��ʱ����ʡǮ���������2673000Ԫ��
��1���蹺��1����Ӱװ���ҪxԪ��һ̨�ʼDZ�������ҪyԪ��������õ�����ϵ������1����Ӱװ��Ǯ=��3̨�ʼDZ����Ե�Ǯ+3000Ԫ��������4����Ӱװ�ķ���+5̨�ʼDZ����Եķ���=80000Ԫ���ɵ�����ϵ�ɵ÷����飬�ⷽ����ɵô𰸡�
��2���蹺������Ӱװ�a�飬����ʼDZ����ԣ�396��a��̨��������ò��ȹ�ϵ��������ʼDZ����Ե�̨���ܹ�����Ӱװ�������3���������Ӱװ�ͱʼDZ������ܷ��á�2700000Ԫ�����ݲ��ȹ�ϵ�ɵò���ʽ�飬�ⲻ��ʽ�飬��������⼴�ɡ�
��3�����ڵ��Ӱװ��������Ӱװ壬������ԣ����ݣ�2���еķ���ȷ����ĵ���������Ӱװ�����������ܷ��á�


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��˾��ij�������Ͷ�Ź�������������ʹ�ã�Ͷ�����ķֲ���Ͷ�ź��ʹ�����ͳ�����£�
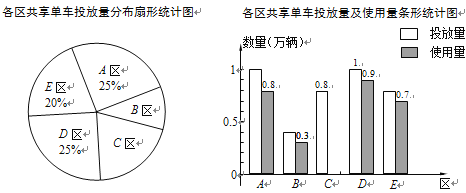
��1���ù�˾��ȫ��һ��Ͷ���� ��������������
��2��������ͳ��ͼ�У�B������Ӧ���ε�Բ�Ľ�Ϊ �㣻
��3���ù�˾��ȫ��Ͷ�ŵĹ���������ʹ����ռͶ������85%�������C������������ʹ��������ȫ����ͳ��ͼ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ƽ����x���ֱ��AC�ֱ�������y1=x2��x��0����y2= ![]() ��x��0����B��C���㣬����C��y���ƽ���߽�y1�ڵ�D��ֱ��DE��AC����y2�ڵ�E����
��x��0����B��C���㣬����C��y���ƽ���߽�y1�ڵ�D��ֱ��DE��AC����y2�ڵ�E���� ![]() = ��
= �� 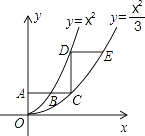
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����(1)��ͬѧΪ�˽�ijС����ͥ�¾���ˮ�������������˸�С�����ּ�ͥ���������������������±�(����)��
�¾��� ˮ��x/m3 | 0�� x��5 | 5�� x��10 | 10�� x��15 | 15�� x��20 | x��20 |
Ƶ��/���� | 12 | 20 | 3 | ||
�ٷֱ� | 12% | 7% |
����С����800����ͥ���ݴ˹��Ƹ�С���¾���ˮ��������10 m3�ļ�ͥ��________����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪AC��BC��BD��AD��AC ��BD ����O��AC=BD��
��֤����1��BC=AD��
��2����OAB�ǵ��������Σ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������������y= ![]() ��x��0����ͼ����һ��A��AB��x���ڵ�B������AO����S��AOB=2����k��ֵΪ�� ��
��x��0����ͼ����һ��A��AB��x���ڵ�B������AO����S��AOB=2����k��ֵΪ�� �� 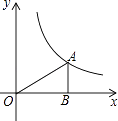
A.2
B.3
C.4
D.5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD�ĶԽ��߽��ڵ�O�������������������ж��ı���ABCD��ƽ���ı����� ��.

A. OA��OC��OB��OD B. ��BAD����BCD��AB��CD
C. AD��BC��AD��BC D. AB��CD��AO��CO
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
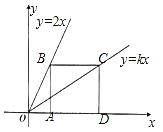
����Ŀ����ͼ����B��C�ֱ���ֱ��y=2x��y=kx�ϣ���A��D��x���ϵ����㣬���ı���ABCD�������Σ�
��1����������ABCD�ı߳�Ϊ2�����B��C������ֱ�Ϊ�� ����
��2����������ABCD�ı߳�Ϊa����k��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�κ���y=kx+b��ͼ���뷴��������y= ![]() ��x��0����ͼ���ڵ�P��n��2������x�ύ�ڵ�A����4��0������y�ύ�ڵ�C��PB��x���ڵ�B����AC=BC��
��x��0����ͼ���ڵ�P��n��2������x�ύ�ڵ�A����4��0������y�ύ�ڵ�C��PB��x���ڵ�B����AC=BC��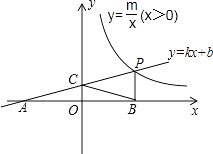
��1����һ�κ����������������Ľ���ʽ��
��2������������ͼ�����Ƿ���ڵ�D��ʹ�ı���BCPDΪ���Σ�������ڣ������D�����ꣻ��������ڣ�˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com