
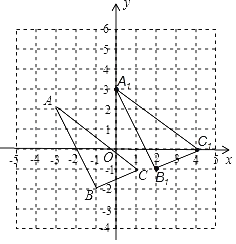
【题目】如图,A(﹣3,2),B(﹣1,﹣2),C(1,﹣1).将△ABC向右平移3个单位长度,然后再向上平移1个单位长度,可以得到△A1B1C1.
(1)△A1B1C1的顶点A1的坐标为 ;顶点C1的坐标为 .
(2)求△A1B1C1的面积.
(3)已知点P在x轴上,以A1、C1、P为顶点的三角形面积为![]() ,则P点的坐标为 .
,则P点的坐标为 .

【答案】(1) (0,3), (4,0);(2)5;(3)(3,0)或(5,0)
【解析】
(1)利用点平移的坐标变换规律写出△A1B1C1三个顶点的坐标,然后描点即可;
(2)用一个矩形的面积分别减去三个三角形的面积得到△A1B1C1的面积;
(3)设P点得坐标为(t,0),利用三角形面积公式,即可得到P点坐标.
解:(1)如图,△A1B1C1为所作,顶点A1的坐标为(0,3);顶点C1的坐标为(4,0),
故答案是:(0,3),(4,0)
(2)计算△A1B1C1的面积=4×4﹣![]() ×2×4﹣
×2×4﹣![]() ×2×1﹣
×2×1﹣![]() ×4×3=5;
×4×3=5;
(3)设P点得坐标为(t,0),
∵以A1、C1、P为顶点得三角形得面积为![]() ,
,
∴![]() ×3×|t﹣4|=
×3×|t﹣4|=![]() ,解得t=3或t=5,
,解得t=3或t=5,
即P点坐标为(3,0)或(5,0).
故答案为:(3,0)或(5,0).


科目:初中数学 来源: 题型:
【题目】为了了解学生关注热点新闻的情况,“两会”期间,小明对班级同学一周内收看“两会”新闻的次数情况作了调查,调查结果统计如图所示(其中男生收看![]() 次的人数没有标出).
次的人数没有标出).
根据上述信息,解答下列各题:
 ×
×
(1)该班级女生人数是__________,女生收看“两会”新闻次数的中位数是________;
(2)对于某个群体,我们把一周内收看某热点新闻次数不低于![]() 次的人数占其所在群体总人数的百分比叫做该群体对某热点新闻的“关注指数”.如果该班级男生对“两会”新闻的“关注指数”比女生低
次的人数占其所在群体总人数的百分比叫做该群体对某热点新闻的“关注指数”.如果该班级男生对“两会”新闻的“关注指数”比女生低![]() ,试求该班级男生人数;
,试求该班级男生人数;
(3)为进一步分析该班级男、女生收看“两会”新闻次数的特点,小明给出了男生的部分统计量(如表).
统计量 | 平均数(次) | 中位数(次) | 众数(次) | 方差 | … |
该班级男生 |
|
|
|
| … |
根据你所学过的统计知识,适当计算女生的有关统计量,进而比较该班级男、女生收看“两会”新闻次数的波动大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c上部分点的横坐标x纵坐标y的对应值如下表,则下列说法中错误的是( ).
x | … | -4 | -3 | -2 | -1 | 0 | 1 | … |
y | … | -37 | -21 | -9 | -1 | 3 | 3 | … |
A.当x>1时y随x的增大而增大
B.抛物线的对称轴为x= ![]()
C.当x=2时y=-1
D.方程ax2+bx+c=0一个负数解x1满足-1<x1<0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y1=a(x+2)2+m过原点,与抛物线y2= ![]() (x﹣3)2+n交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于点B,C.下列结论:①两条抛物线的对称轴距离为5;②x=0时,y2=5;③当x>3时,y1﹣y2>0;④y轴是线段BC的中垂线.正确结论是(填写正确结论的序号).
(x﹣3)2+n交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于点B,C.下列结论:①两条抛物线的对称轴距离为5;②x=0时,y2=5;③当x>3时,y1﹣y2>0;④y轴是线段BC的中垂线.正确结论是(填写正确结论的序号). 
查看答案和解析>>
科目:初中数学 来源: 题型:
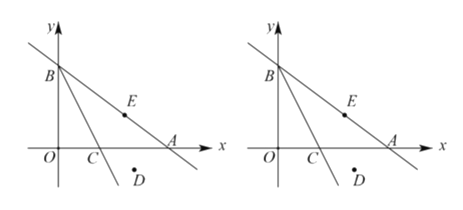
【题目】已知直线![]() 与
与![]() 轴,
轴,![]() 轴分别交于点
轴分别交于点![]() ,将
,将![]() 对折,使点
对折,使点![]() 的对称点
的对称点![]() 落在直线
落在直线![]() 上,折痕交
上,折痕交![]() 轴于点
轴于点![]() .
.
(1)求点![]() 的坐标;
的坐标;
(2)若已知第四象限内的点![]() ,在直线
,在直线![]() 上是否存在点
上是否存在点![]() ,使得四边形
,使得四边形![]() 为平行四边形?若存在,求出点
为平行四边形?若存在,求出点![]() 的坐标;若不存在,说明理由;
的坐标;若不存在,说明理由;
(3)设经过点![]() 且与
且与![]() 轴垂直的直线与直线
轴垂直的直线与直线![]() 的交点为
的交点为![]() 为线段
为线段![]() 上一点,求
上一点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣(x﹣1)2+c与x轴交于A,B(A,B分别在y轴的左右两侧)两点,与y轴的正半轴交于点C,顶点为D,已知A(﹣1,0).
(1)求点B,C的坐标;
(2)判断△CDB的形状并说明理由;
(3)将△COB沿x轴向右平移t个单位长度(0<t<3)得到△QPE.△QPE与△CDB重叠部分(如图中阴影部分)面积为S,求S与t的函数关系式,并写出自变量t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c的图象如图所示,以下结论:①abc>0;②4ac<b2;③2a+b>0;④其顶点坐标为( ![]() ,﹣2);⑤当x<
,﹣2);⑤当x< ![]() 时,y随x的增大而减小;⑥a+b+c>0正确的有( )
时,y随x的增大而减小;⑥a+b+c>0正确的有( )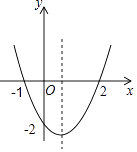
A.3个
B.4个
C.5个
D.6个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市经济技术开发区某智能手机有限公司接到生产300万部智能手机的订单,为了尽快交货,增开了一条生产线,实际每月生产能力比原计划提高了50%,结果比原计划提前5个月完成交货,求每月实际生产智能手机多少万部.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年5月12日是我国第11个全国防灾减灾日,重庆某中学为普及推广全民防灾减灾知识和避灾自救技能,开展了“提高灾害防治能力,构筑生命安全防线”知识竞赛活动.初一、初二年级各500人,为了调查竞赛情况,学校进行了抽样调查,过程如下,请根据表格回答问题.
收集数据:
从初一、初二年级各抽取20名同学的测试成绩(单位:分),记录如下:
初一:68、79、100、98、98、86、88、99、100、93、90、100、80、76、84、98、99、86、98、90
初二:92、89、100、99、98、94、100、62、100、86、75、98、89、100、100、68、79、100、92、89
整理数据:
表一
分数段 |
|
|
|
|
初一人数 | 1 |
|
| 12 |
初二人数 | 2 | 2 | 4 | 12 |
分析数据:
表二
种类 | 平均数 | 中位数 | 众数 | |
初一 | 90.5 | 91.5 |
| 84.75 |
初二 | 90.5 |
| 100 | 123.05 |
得出结论:
(1)在表中:![]() _______,
_______,![]() _______,
_______,![]() _______,
_______,![]() _______;
_______;
(2)得分情况较稳定的是___________(填初一或初二);
(3)估计该校初一、初二年级学生本次测试成绩中可以得满分的人数共有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com