
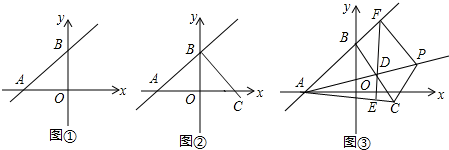
���� ��1����$\sqrt{b-6}$=��a+8��2-$\sqrt{6-b}$������a=-8��b=6������ȷ��A��B��������꣺A��-8��0����B��0��6���������ɵã�OA=8��OB=6��Ȼ����ݹ��ɶ�������AB�ij���
��2������C��CM��y�ᣬ����ΪM������AAS��֤��ABO�ա�BCM��Ȼ�����ȫ�������εĶ�Ӧ����ȣ��ɵã�CM=OB=6��BM=OA=8���Ӷ�ȷ����C�����ꣻ
��3������D��DN��y�ᣬ����ΪN����D��BC���е㣬�ɵ�DN�ǡ�BCM����λ�ߣ�������ȷ����D�����꣬Ȼ���ô���ϵ�����ֱ����ֱ��AB��ֱ��AC��ֱ��AD��ֱ��EF�Ĺ�ϵʽ��Ȼ���ɵ�F��ֱ��AB��ֱ��EF�Ľ��㣬��ֱ��AB��ֱ��EF�Ĺ�ϵʽ���������������F�����꣬Ȼ�����P��x��y����Ȼ�����������ľ��빫ʽ���ɱ�ʾPF2-PC2�����㼴�ɣ�
��� �⣺��1����$\sqrt{b-6}$=��a+8��2-$\sqrt{6-b}$��
��b-6��0��6-b��0��
��b=6��
�ࣨa+8��2=0��
��a=-8��
��A��-8��0����B��0��6����
��OA=8��OB=6��
��Rt��ABO�У��ɹ��ɶ����ã�
AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=10��
��2������C��CM��y�ᣬ����ΪM����ͼ��ʾ2��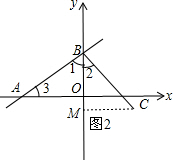 ��CB��AB��
��CB��AB��
���1+��2=90�㣬
�ߡ�1+��3=90�㣬
���2=��3��
��CM��y�ᣬ
���BMC=90�㣬
���BMC=��AMB��
�ڡ�ABO�͡�BCM�У�
��$\left\{\begin{array}{l}{��2=��3}\\{��CMB=��BOA}\\{AB=BC}\end{array}\right.$
���ABO�ա�BCM��AAS����
��CM=OB=6��BM=OA=8��
��OM=BM-BO=8-6=2��
�ߵ�C�ڵ������ޣ�
��C��6��-2����
��3������P������AD���˶�ʱ��PF2-PC2��ֵ�������ı䣮
����D��DN��y�ᣬ����ΪN����ͼ3��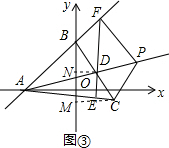 ��D��BC���е㣬
��D��BC���е㣬
��DN�ǡ�BCM����λ�ߣ�
��DN=$\frac{1}{2}$MC=3��BN=$\frac{1}{2}$BM=4��
��ON=OB-BN=6-4=2��
��D��3��2����
��ֱ��AB�Ĺ�ϵʽΪ��yAB=kx+b��
��A��-8��0����B��0��6��������ʽ�ã�
k=$\frac{3}{4}$��b=6��
��yAB=$\frac{3}{4}$x+6��
��ֱ��AC�Ĺ�ϵʽΪ��yAC=kx+b��
��A��-8��0����C��6��-2��������ʽ�ã�
k=$-\frac{1}{7}$��b=-$\frac{8}{7}$��
��yAC=-$\frac{1}{7}$x-$\frac{8}{7}$��
��ֱ��AD�Ĺ�ϵʽΪ��yAD=kx+b��
��A��-8��0����D��3��2��������ʽ�ã�
k=$\frac{2}{11}$��b=$\frac{16}{11}$��
��yAD=$\frac{2}{11}$x+$\frac{16}{11}$��
��EF��AC��
����ֱ��EF�Ĺ�ϵʽΪ��yEF=7x+b��
��D����ֱ��EF�ϣ�
�ཫD��3��2������yEF=7x+b���ã�b=-19��
��yEF=7x-19��
��ֱ��AB��ֱ��EF�Ĺ�ϵʽ����������ã�$\left\{\begin{array}{l}{y=\frac{3}{4}x+6}\\{y=7x-19}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{x=4}\\{y=9}\end{array}\right.$��
��F��4��9����
��P��x��y����
��PF2=��x-4��2+��y-9��2��PC2=��x-6��2+��y+2��2��
��PF2-PC2=4x-22y+57��
��P��x��y����ֱ��AD�ϣ�
��P��x��y������yAD=$\frac{2}{11}$x+$\frac{16}{11}$���ã�
y=$\frac{2}{11}$x+$\frac{16}{11}$��
��y=$\frac{2}{11}$x+$\frac{16}{11}$������PF2-PC2=4x-22y+57���ã�
��PF2-PC2=4x-22y+57=4x-22��$\frac{2}{11}$x+$\frac{16}{11}$��+57=25��
�൱��P������AD���˶�ʱ��PF2-PC2��ֵ�������ı䣬PF2-PC2��ֵ��25��
���� ������һ�κ������ۺ��⣬��Ҫ�������ô���ϵ������һ�κ����Ĺ�ϵʽ�����ɶ�����Ӧ�ã�ȫ�������ε��ж������ʣ�������ֱ�ߵĽ������⣬�����ľ��빫ʽ��֪ʶ����������ľ��빫ʽ�ǽ���Ĺؼ���ע�⣺����֪����A��x1��y1����B��x2��y2������|AB|=$\sqrt{{��x}_{1}-{x}_{2}��^{2}+��{y}_{1}-{y}_{2}��^{2}}$��


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{\sqrt{8}}{3}$ | B�� | $\frac{{2\sqrt{2}}}{{\sqrt{9}}}$ | C�� | $\frac{2}{3}$ | D�� | $\frac{2\sqrt{2}}{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ij���в���Ϊ���˽���У�������Ķ��̿������״�������ȡijУ���ֳ���ѧ�������˵��飬����������ݻ��Ƴ����²�������ͳ�Ʊ��������ͼ���е���Ϣ����������⣺
ij���в���Ϊ���˽���У�������Ķ��̿������״�������ȡijУ���ֳ���ѧ�������˵��飬����������ݻ��Ƴ����²�������ͳ�Ʊ��������ͼ���е���Ϣ����������⣺| ��� | ���� | ռ���������� |
| ���� | a | b |
| һ�� | 57 | 0.285 |
| ������ | c | 0.36 |
| ˵����� | 9 | 0.045 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
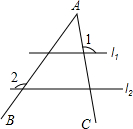 ��ͼ����A��ƽ��ֱ��l1��l2���أ�����1=100�㣬��2=125�㣬���A�Ķ����ǣ�������
��ͼ����A��ƽ��ֱ��l1��l2���أ�����1=100�㣬��2=125�㣬���A�Ķ����ǣ�������| A�� | 25�� | B�� | 30�� | C�� | 35�� | D�� | 45�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
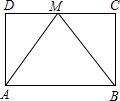 ��ͼ����?ABCD�У���MΪCD�ߵ��е㣬��ABM�ǵȱ������Σ���֤��?ABCD�Ǿ��Σ�
��ͼ����?ABCD�У���MΪCD�ߵ��е㣬��ABM�ǵȱ������Σ���֤��?ABCD�Ǿ��Σ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
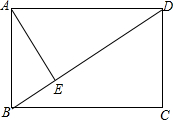 ��ͼ��ʾ���ھ���ABCD�У�AD�ij�Ϊ8cm���Խ���BD��AB�߳�4cm��
��ͼ��ʾ���ھ���ABCD�У�AD�ij�Ϊ8cm���Խ���BD��AB�߳�4cm���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
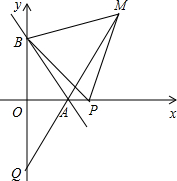 ��ͼ��ֱ��AB��x���������ڵ�A��a��0������y���������ڵ�B��0��b������a��b���㣨a-b��2+$\sqrt{{b}^{2}-16}$=0
��ͼ��ֱ��AB��x���������ڵ�A��a��0������y���������ڵ�B��0��b������a��b���㣨a-b��2+$\sqrt{{b}^{2}-16}$=0�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com