
| A.y=(x﹣2)2 | B.y=(x﹣2)2+6 | C.y=x2+6 | D.y=x2 |
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案科目:初中数学 来源:不详 题型:解答题
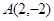 和点
和点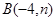 在抛物线
在抛物线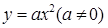 上.
上. 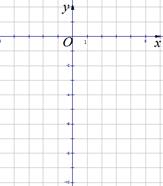
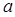 的值及点
的值及点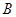 的坐标;
的坐标;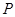 在
在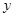 轴上,且满足△
轴上,且满足△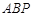 是以
是以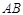 为直角边的直角三角形,求点
为直角边的直角三角形,求点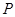 的坐标;
的坐标;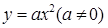 ,记平移后点A的对应点为
,记平移后点A的对应点为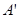 ,点B的对应点为
,点B的对应点为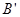 . 点M(2,0)在x轴上,当抛物线向右平移到某个位置时,
. 点M(2,0)在x轴上,当抛物线向右平移到某个位置时,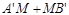 最短,求此时抛物线的函数解析式.
最短,求此时抛物线的函数解析式.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
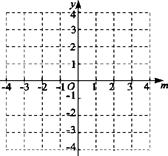
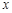 的取值范围.
的取值范围.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
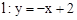 与y轴交于点A,抛物线
与y轴交于点A,抛物线 经过点A,其顶点为B,另一抛物线
经过点A,其顶点为B,另一抛物线 的顶点为D,两抛物线相交于点C
的顶点为D,两抛物线相交于点C
 的理由;
的理由; ,求m的值.
,求m的值.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
 的图像向左平移2个单位再向下平移4个单位,所得函数表达式是
的图像向左平移2个单位再向下平移4个单位,所得函数表达式是 ,我们来解释一下其中的原因:不妨设平移前图像上任意一点P经过平移后得到点P’,且点P’的坐标为
,我们来解释一下其中的原因:不妨设平移前图像上任意一点P经过平移后得到点P’,且点P’的坐标为 ,那么P’点反之向右平移2个单位,再向上平移4个单位得到点
,那么P’点反之向右平移2个单位,再向上平移4个单位得到点 ,由于点P是二次函数
,由于点P是二次函数 的图像上的点,于是把点P(x+2,y+4)的坐标代入
的图像上的点,于是把点P(x+2,y+4)的坐标代入 再进行整理就得到
再进行整理就得到 .类似的,我们对函数
.类似的,我们对函数 的图像进行平移:先向右平移1个单位,再向上平移3个单位,所得图像的函数表达式为_____.
的图像进行平移:先向右平移1个单位,再向上平移3个单位,所得图像的函数表达式为_____.查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com