
 已知△ABC中,∠ABC=40°,∠ACB=80°,O、I、H分别是△ABC的外心、内心和垂心,求证:
已知△ABC中,∠ABC=40°,∠ACB=80°,O、I、H分别是△ABC的外心、内心和垂心,求证:分析 (1)延长BO交外接圆于E,连接BI、BH、CI、OC、EC,由圆周角定理得出∠BOC=2∠BAC=120°,根据三角形内心的性质求出∠BIC=120°,同理根据垂心的性质得出∠BHC=120°,即可得出B,C,O,H、I五点共圆,进而求得∠IBC=∠HBC=∠OBI=10°,即可证得结论;
(2)构造以垂心H为顶点的平行四边形AHCE,再由平行四边形的性质及角之间的关系即可求解.
解答 证明:(1)延长BO交外接圆于E,连接BI、BH、CI、OC、EC,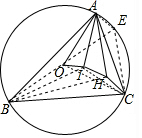
∵∠ABC=40°,∠ACB=80°,
∴∠BAC=60°,
∵O是三角形的外心,
∴∠BOC=2∠BAC=120°(同弧所对的圆心角等于圆周角的两倍),
∵I是△ABC的内心,
∴∠IBC=$\frac{1}{2}$∠ABC=20°,∠ICB=$\frac{1}{2}$∠ACB=40°,
∴∠BIC=120°.
又∵垂心为点H,
∴∠BCH=50°,∠HBC=10°,
∴∠BHC=120°,
∴BE⊥AC,
∴∠BAE=90°,
∴∠ABE=90°-∠BAC=90°-60°=30°,
∴∠BOC=∠BIC=∠BHC,
又∵O,I,H在BC边同侧,
∴B,C,O,H、I五点共圆.
∵O是外心,
∴BE是直径,
∴∠BCE=90°,
∵∠BEC=∠BAC=60°,
∴∠EBC=∠30°,
∵∠IBC=20°,∠HBC=10°,
∴∠IBC=∠HBC=∠OBI=10°,
∴OI=IH=HC;
(2)连接AE,
∵H是垂心.
∴AH⊥BC,
∵CE⊥BC,
∴AH∥CE.
同理CH∥AE.
∴四边形AHCE为平行四边形,
∴AH=CE.
又∠BEC=∠A=60°,从而∠EBC=∠30°.
所以EC=$\frac{1}{2}$BE=OA,
故AH=OA.
点评 本题主要考查了三角形外心、内心、垂心的性质,平行四边形的判定及性质,能够结合题意通过作辅助线建立关系,再结合已知的关系最终得出结论.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,有抛物线y=ax2+bx+3,已知OA=OC=3OB,动点P在过A、B、C三点的抛物线上.
如图,在平面直角坐标系中,有抛物线y=ax2+bx+3,已知OA=OC=3OB,动点P在过A、B、C三点的抛物线上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
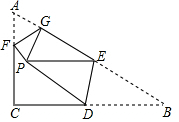 如图所示,在Rt△ABC纸片中,∠C=90°,∠B=30°,AC=6,将∠A、∠B向内翻折,使顶点A、B重合于一点P,折痕分别为FG和DE,若PE∥BC,BD=4,则PF=10-4$\sqrt{3}$.
如图所示,在Rt△ABC纸片中,∠C=90°,∠B=30°,AC=6,将∠A、∠B向内翻折,使顶点A、B重合于一点P,折痕分别为FG和DE,若PE∥BC,BD=4,则PF=10-4$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2cos$\frac{180°}{n}$ | B. | 2sin$\frac{180°}{n}$ | C. | 2tan$\frac{180°}{n}$ | D. | 2cot$\frac{180°}{n}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 15.5cm | B. | 6.2cm | C. | 3.1cm | D. | 2.6cm |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com