
 ��ͼ����Rt��ABC�У���ABC=90�㣬AB=12��BC=6����H�ڱ�AB�ϣ���BH=8������HC������F��ÿ��2����λ���ȵ��ٶȣ��ӵ�B�����ر�BH���H�˶�����ʱֱ��FG��BC��HG�ڵ�G����x��ʱ��FG�ij���Ϊy
��ͼ����Rt��ABC�У���ABC=90�㣬AB=12��BC=6����H�ڱ�AB�ϣ���BH=8������HC������F��ÿ��2����λ���ȵ��ٶȣ��ӵ�B�����ر�BH���H�˶�����ʱֱ��FG��BC��HG�ڵ�G����x��ʱ��FG�ij���Ϊy���� ��1��������ã�BF=2x������FG��BC֤�á�HFG�ס�HBC���б���ʽ�ó�y��x�ĺ�������ʽ��
��2���ȸ���ͬ�ǵ����Ǻ���ֵ�б���ʽ��ʾAD�ij������ݾ��ε����=����������ʽ��S��x�Ĺ�ϵʽ������ֵ���ɣ�
��� �⣺��1��������ã�BF=2x����FH=8-2x��
��FG��BC��
���HFG�ס�HBC��
��$\frac{HF}{HB}$=$\frac{FG}{BC}$��
��$\frac{8-2x}{8}=\frac{y}{6}$��
��8y=6��8-2x����
y=-$\frac{3}{2}$x+6��
��2��DE=FG=-$\frac{3}{2}x$+6��
tan��A=$\frac{DE}{AD}=\frac{BC}{AB}$��
��$\frac{-\frac{3}{2}x+6}{AD}$=$\frac{6}{12}$��
��AD=-3x+12��
��DF=AB-AD-BF=12-��-3x+12��-2x=x��
��S=S����DEGF=FG•DF=x��-$\frac{3}{2}$x+6��=-$\frac{3}{2}$x2+6x=-$\frac{3}{2}$��x2-4x+4-4��=-$\frac{3}{2}$��x-2��2+6��
��-$\frac{3}{2}$��0��
��S�����ֵ��
��0��x��4��
�൱x=2ʱ��S�����ֵΪ6��
���� �����Ǿ��κͶ��κ������ۺ��⣬�ѶȲ�����Ҫ�����˾��Ρ����κ��������ʣ�֪�����εĶԱ���ȣ����ĸ���Ϊֱ�ǣ������Ϊ������������Ƕ����˶����⣬��������Ҫ��Ū��ö�����˶�·�ߡ�ʱ�䡢�ٶȣ����ʾ��·�̣�������κ������ϣ����������ʽ�������������ת��Ϊ���κ�������ֵ���⣬ʹ����ӭ�ж��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3x2y��2xy2 | B�� | $\frac{1}{3}$x4y��$\frac{1}{2}$yx4 | ||
| C�� | -2a��0 | D�� | $\frac{1}{2}$��a2bc3��-3a2cb3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
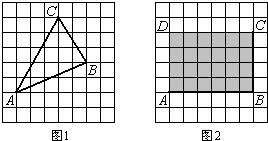
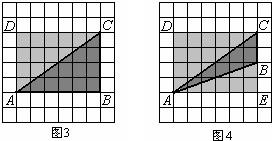
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
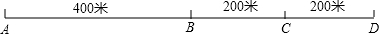
| A�� | D�� | B�� | A�� | C�� | AB����֮�� | D�� | BC����֮�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -5 | B�� | 5 | C�� | 13 | D�� | -13 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{2\frac{2}{3}}$=2$\sqrt{\frac{2}{3}}$ | B�� | $\frac{1}{a+b}=\frac{c}{��a+b��c}$ | C�� | a$\sqrt{-\frac{1}{a}}$=-$\sqrt{-a}$ | D�� | $\frac{-c}{-a+b}=\frac{c}{a-b}$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com