
 实验数据显示,一般成人喝半斤低度白酒后,1.5小时内其血液中酒精含量y(毫克/百毫升)与时间x(时)的关系可近似地用正比例函数y=100x刻画;1.5小时后(包括1.5小时)y与x可近似地用反比例函数y=$\frac{k}{x}$(k>0)刻画(如图所示).
实验数据显示,一般成人喝半斤低度白酒后,1.5小时内其血液中酒精含量y(毫克/百毫升)与时间x(时)的关系可近似地用正比例函数y=100x刻画;1.5小时后(包括1.5小时)y与x可近似地用反比例函数y=$\frac{k}{x}$(k>0)刻画(如图所示).分析 (1)利用待定系数法即可解决问题.
(2)求出y=80时,相应的两个x的值即可解决问题.
(3)求出y=20时,相应的两个x的值,求出时间差即可判断.
解答 解:(1)∵当x=5时,y=45,
∴45=$\frac{k}{5}$,
∴k=225.
(2)当y=80时,80=100x,解得x=0.8,
80=$\frac{225}{x}$,解得x=2.8125小时,
∴肝部被严重损伤持续时间=2.8125-0.8=2.0125小时.
(3)当y=20时,20=100x,解得x=0.2,
20=$\frac{225}{x}$,解得x=11.25,
∵11.25-0.2=11.05小时,
∵20:00在家喝完半斤低度白酒,第二天早上7:00上班,这个时间差是11小时,
11<11.05,
∴第二天早上7:00不能驾车去上班.
点评 本题考查反比例函数的应用、一次函数的应用等知识,解题的关键是灵活掌握待定系数法确定函数解析式,学会利用函数解决实际问题,属于中考常考题型.


 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
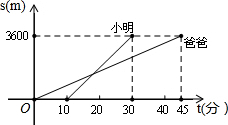 星期天,小明和爸爸去大剧院看电影.爸爸步行先走,小明在爸爸离开家一段时间后骑自行车去,两人按相同的路线前往大剧院,他们所走的路程s(米)和时间t(分)的关系如图所示.则小明追上爸爸时,爸爸共走了( )
星期天,小明和爸爸去大剧院看电影.爸爸步行先走,小明在爸爸离开家一段时间后骑自行车去,两人按相同的路线前往大剧院,他们所走的路程s(米)和时间t(分)的关系如图所示.则小明追上爸爸时,爸爸共走了( )| A. | 12分钟 | B. | 15分钟 | C. | 18分钟 | D. | 21分钟 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,已知O是等边△ABC内一点,OD∥BC,OE∥AC,OF∥AB,点D,E,F分别在AB,BC,CA上.若OD:OE:OF=1:2:3,则S四边形ADOF:S四边形BEOD:S四边形CFOE等于( )
如图,已知O是等边△ABC内一点,OD∥BC,OE∥AC,OF∥AB,点D,E,F分别在AB,BC,CA上.若OD:OE:OF=1:2:3,则S四边形ADOF:S四边形BEOD:S四边形CFOE等于( )| A. | 1:2:3 | B. | 1:4:9 | C. | 7:8:15 | D. | 7:8:21 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com