
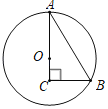
【题目】如图,△ABC中,∠C=90°,∠B=60°,在AC边上取点O画圆,使⊙O经过A、B两点,下列结论中:①AO=BC;②AO=2CO;③延长BC交⊙O与D,则A、B、D是⊙O的三等分点;④以O为圆心,以OC为半径的圆与AB相切.正确的序号是______.
【答案】.②③④
【解析】
连接OB,可得∠ABO=30°,则∠OBC=30°,根据三角函数cos∠OBC=![]() ,则BC=
,则BC=![]() OB,根据直角三角形的性质得OC=
OB,根据直角三角形的性质得OC=![]() OB=
OB=![]() OA,根据垂径定理,得直线AC是弦BD的垂直平分线,则点A、B、D将⊙O的三等分,因为点O在∠ABC的角平分线上,所以点O到直线AB的距离等于OC的长.
OA,根据垂径定理,得直线AC是弦BD的垂直平分线,则点A、B、D将⊙O的三等分,因为点O在∠ABC的角平分线上,所以点O到直线AB的距离等于OC的长.
解:连接OB,
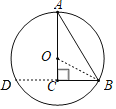
∵OA=OB,
∴∠A=∠ABO,
∵∠C=90°,∠ABC=60°,
∴∠ABO=∠A=30°,
∴∠OBC=30°,
∵cos∠OBC=![]() ,
,
∴BC=![]() OB,
OB,
即BC=![]() OA,
OA,
故①错误,
∵∠OBC=30°,
∴OC=![]() OB=
OB=![]() OA,
OA,
即OA=2OC,
故②正确;
延长BC交⊙O于D,
∵AC⊥BD,
∴AD=AB,
∴△ABD为等边三角形,
∴![]() =
=![]() =
=![]() ,
,
∴点A、B、D将⊙O的三等分;
故③正确;
∵∠ABO=∠OBC=30°,
∴点O在∠ABC的角平分线上,
∴点O到直线AB的距离等于OC的长,
即以O为圆心,以OC为半径的圆与AB相切.
故④正确.
故答案为:②③④.


科目:初中数学 来源: 题型:
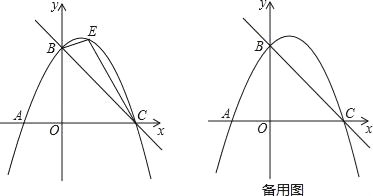
【题目】如图,直线y=﹣![]() x+4与x轴交于点C,与y轴交于点B,抛物线y=ax2+
x+4与x轴交于点C,与y轴交于点B,抛物线y=ax2+![]() x+c经过B、C两点.
x+c经过B、C两点.
(1)求抛物线的解析式;
(2)如图,点E是直线BC上方抛物线上的一动点,当△BEC面积最大时,请求出点E的坐标;
(3)在(2)的结论下,过点E作y轴的平行线交直线BC于点M,连接AM,点Q是抛物线对称轴上的动点,在抛物线上是否存在点P,使得以P、Q、A、M为顶点的四边形是平行四边形?如果存在,请直接写出点P的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:各类方程的解法
求解一元一次方程,根据等式的基本性质,把方程转化为x=a的形式.求解二元一次方程组,把它转化为一元一次方程来解;类似的,求解三元一次方程组,把它转化为解二元一次方程组.求解一元二次方程,把它转化为两个一元一次方程来解.求解分式方程,把它转化为整式方程来解,由于“去分母”可能产生增根,所以解分式方程必须检验.各类方程的解法不尽相同,但是它们有一个共同的基本数学思想![]() 转化,把未知转化为已知.
转化,把未知转化为已知.
用“转化”的数学思想,我们还可以解一些新的方程.例如,一元三次方程x3+x2-2x=0,可以通过因式分解把它转化为x(x2+x-2)=0,解方程x=0和x2+x-2=0,可得方程x3+x2-2x=0的解.
(1)问题:方程x3+x2-2x=0的解是x1=0,x2= ,x3= ;
(2)拓展:用“转化”思想求方程![]() 的解;
的解;
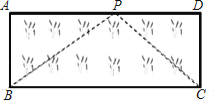
(3)应用:如图,已知矩形草坪ABCD的长AD=8m,宽AB=3m,小华把一根长为10m的绳子的一端固定在点B,沿草坪边沿BA,AD走到点P处,把长绳PB段拉直并固定在点P,然后沿草坪边沿PD、DC走到点C处,把长绳剩下的一段拉直,长绳的另一端恰好落在点C.求AP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小李驾驶小汽车匀速地从A地行驶到B地,行驶里程为360千米,设小汽车的行驶时间为t(单位:小时),行驶速度为v(单位:千米/小时),且全程速度限定为不超过120千米/小时.
(1)求v关于t的函数表达式(不用写取值范围);
(2)小李上午8点驾驶小汽车从A地出发.
①小李需在当天12点至13点间到达B地,求小汽车行驶速度v的范围.
②小李能否在当天11点30分前到达B地?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
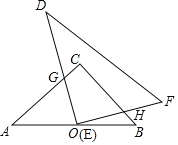
【题目】如图,在等腰直角三角形ABC中,∠C=90°,AB=8![]() ,点O是AB的中点.将一个边长足够大的Rt△DEF的直角顶点E放在点O处,并将其绕点O旋转,始终保持DE与AC边交于点G,EF与BC边交于点H.
,点O是AB的中点.将一个边长足够大的Rt△DEF的直角顶点E放在点O处,并将其绕点O旋转,始终保持DE与AC边交于点G,EF与BC边交于点H.
(1)当点G在AC边什么位置时,四边形CGOH是正方形.
(2)等腰直角三角ABC的边被Rt△DEF覆盖部分的两条线段CG与CH的长度之和是否会发生变化,如不发生变化,请求出CG与CH之和的值:如发生变化,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】城市中“打车难”一直是人们关注的一个社会热点问题.近几年来,“互联网+”战略与传统出租车行业深度融合,“优步”、“滴滴出行”等打车软件就是其中典型的应用,名为“数据包络分析”(简称DEA)的一种效率评价方法,可以很好地优化出租车资源配置,为了解出租车资源的“供需匹配”,北京、上海等城市对每天24个时段的DEA值进行调查,调查发现,DEA值越大,说明匹配度越好.在某一段时间内,北京的DEA值y与时刻t的关系近似满足函数关系![]() (a,b,c是常数,且
(a,b,c是常数,且![]() ≠0),如图记录了3个时刻的数据,根据函数模型和所给数据,当“供需匹配”程度最好时,最接近的时刻t是( )
≠0),如图记录了3个时刻的数据,根据函数模型和所给数据,当“供需匹配”程度最好时,最接近的时刻t是( )
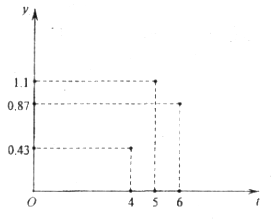
A. 4.8 B. 5 C. 5.2 D. 5.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△AOB中,∠AOB=90°,点A的坐标为(2,1),BO=2![]() ,反比例函数y=
,反比例函数y=![]() 的图象经过点B,则k的值为( )
的图象经过点B,则k的值为( )
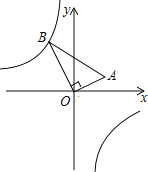
A.﹣2B.﹣4C.4D.﹣8
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com