
【题目】如果直线l与⊙O有公共点,那么直线l与⊙O的位置关系是 ( )
A. 相交 B. 相切 C. 相离 D. 相切或相交
 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案科目:初中数学 来源: 题型:
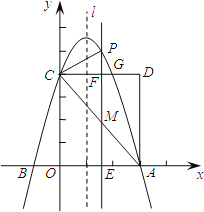
【题目】如图,抛物线![]() (a≠0)交x轴于A、B两点,A点坐标为(3,0),与y轴交于点C(0,4),以OC、OA为边作矩形OADC交抛物线于点G.
(a≠0)交x轴于A、B两点,A点坐标为(3,0),与y轴交于点C(0,4),以OC、OA为边作矩形OADC交抛物线于点G.
(1)求抛物线的解析式;
(2)抛物线的对称轴l在边OA(不包括O、A两点)上平行移动,分别交x轴于点E,交CD于点F,交AC于点M,交抛物线于点P,若点M的横坐标为m,请用含m的代数式表示PM的长;
(3)在(2)的条件下,连结PC,则在CD上方的抛物线部分是否存在这样的点P,使得以P、C、F为顶点的三角形和△AEM相似?若存在,求出此时m的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
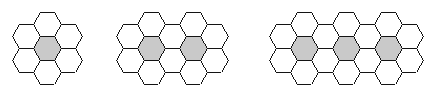
【题目】用黑白两种颜色的正六边形地砖按如下所示的规律拼成若干图案:
![]()
![]()
![]()
⑴ 当黑砖n=1时,白砖有_______块,当黑砖n=2时,白砖有________块,
当黑砖n=3时,白砖有_______块.
⑵ 第n个图案中,白色地砖共 块.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1所示,已知:点![]() 在双曲线
在双曲线![]() :
:![]() 上,直线
上,直线![]() ,直线
,直线![]() 与
与![]() 关于原点成中心对称,
关于原点成中心对称,![]() 两点间的连线与曲线
两点间的连线与曲线![]() 第一象限内的交点为
第一象限内的交点为![]() ,
,![]() 是曲线
是曲线![]() 上第一象限内异于
上第一象限内异于![]() 的一动点,过
的一动点,过![]() 作
作![]() 轴平行线分别交
轴平行线分别交![]() ,
,![]() 于
于![]() 两点.
两点.
(1)求双曲线![]() 及直线
及直线![]() 的解析式;
的解析式;
(2)求证:![]() ;
;
(3)如图2所示,![]() 的内切圆与
的内切圆与![]() 三边分别相切于点
三边分别相切于点![]() ,求证:点
,求证:点![]() 与点
与点![]() 重合.(参考公式:在平面坐标系中,若有点
重合.(参考公式:在平面坐标系中,若有点![]() ,
,![]() ,则A、B两点间的距离公式为=
,则A、B两点间的距离公式为=![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在平面直角坐标系xoy中,直线y=2x+4与y轴交于A点,与x轴交于B点,抛物线C1:y=-![]() x+bx+c过A、B两点,与x轴另一交点为C。
x+bx+c过A、B两点,与x轴另一交点为C。
(1)(3分)求抛物线解析式及C点坐标。
(2)(4分)向右平移抛物线C1,使平移后的抛物线C2恰好经过△ABC的外心,抛物线C1、C2相交于点D,求四边形AOCD的面积。
(3)(5分)已知抛物线C2的顶点为M,设P为抛物线C1对称轴上一点,Q为抛物线C1上一点,是否存在以点M、Q、P、B为顶点的四边形为平行四边形,若存在,直接写出P点坐标,不存在,请说明理由。


图(1) 图(2)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com