
 函数y=x的图象与函数y=
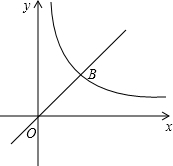
函数y=x的图象与函数y= 的图象在第一象限内交于点B,点C是函数y=
的图象在第一象限内交于点B,点C是函数y= 在第一象限图象上的一个动点,当△OBC的面积为3时,点C的横坐标是________.
在第一象限图象上的一个动点,当△OBC的面积为3时,点C的横坐标是________.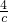 ),由反比例函数k的几何意义求出三角形BOE与三角形COF面积都为2,再由三角形BOC面积为3,得到四边形BCOE面积为5,而四边形BCOE面积由三角形COF与梯形BCFE面积之和求出,利用梯形面积公式列出关于c的方程,求出方程的解得到c的值;当C在B下方时,如图2所示,连接BC,OC,作CF⊥x轴,BE⊥x轴,同理求出c的值,综上,得到满足题意C得横坐标.
),由反比例函数k的几何意义求出三角形BOE与三角形COF面积都为2,再由三角形BOC面积为3,得到四边形BCOE面积为5,而四边形BCOE面积由三角形COF与梯形BCFE面积之和求出,利用梯形面积公式列出关于c的方程,求出方程的解得到c的值;当C在B下方时,如图2所示,连接BC,OC,作CF⊥x轴,BE⊥x轴,同理求出c的值,综上,得到满足题意C得横坐标.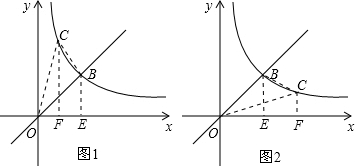
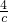 ),
), 在第一象限交于B点,
在第一象限交于B点, •(2-c)•(
•(2-c)•(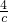 +2)=5,
+2)=5, •(c-2)•(
•(c-2)•(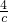 +2)=5,
+2)=5,

科目:初中数学 来源: 题型:
| k | x |
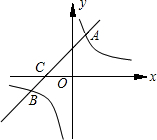 次函数y=mx+b的图象与x轴交于点C.
次函数y=mx+b的图象与x轴交于点C.查看答案和解析>>
科目:初中数学 来源: 题型:
 已知反比例函数y=
已知反比例函数y=| k | x |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2010•皇姑区二模)如图,已知反比例函数y=
(2010•皇姑区二模)如图,已知反比例函数y=| k1 | x |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知反比例函数y=
如图,已知反比例函数y=| k1 | x |
查看答案和解析>>
科目:初中数学 来源: 题型:
 为M,又正比例函数y=kx的图象与二次函数相交于两点D、E,且P是线段DE的中点.
为M,又正比例函数y=kx的图象与二次函数相交于两点D、E,且P是线段DE的中点.| 93 |
| 16 |
| x1+x2 |
| 2 |
| y1+y2 |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com