练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

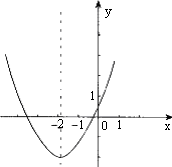
    如下图是抛物线y＝ax2＋bx＋c在平面直角坐标系中的图像．有下列结论：①c＞0，②a＋b＋c＞0，③b2－4ac＜0，④abc＜0，⑤4a＞c．其中所有正确结论的序号是(　　)．

    [　　]

    A．①②

    B．①④

    C．①②⑤

    D．①③⑤

    答案：C
    解析：

    　　解：∵抛物线y＝ax2＋bx＋c交y轴于正半轴，

    　　∴c＞0，

    　　∴①正确；

    　　∵当x＝1时，y＝a＋b＋c＞0，

    　　∴②正确；

    　　∵抛物线与x轴有两个交点，

    　　∴方程ax2＋bx＋c＝0(a≠0)有两个不相等的实数根，

    　　∴△＝b2－4ac＞0，

    　　∴③不正确；

    　　∵抛物线y＝ax2＋bx＋c的开口向上，

    　　∴a＞0，

    　　∵－＜0，

    　　∴b＞0，

    　　∴abc＞0，

    　　∴④不正确；

    　　∵－＝－2

    　　∴b2＝4a，

    　　由b2－4ac＞0，得

    　　16a2－4ac＞0，

    　　∴4a－c＞0，

    　　即4a＞c．

    　　∴⑤正确．

    　　综上知，①②⑤正确，选C．

    　　注：把握函数图像的特征，挖掘图像蕴涵的各种信息，才能有效地阅读函数图像，正确作出解答和判断．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2011年广西梧州市初中毕业升学考试数学试卷 题型：013

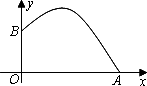
    2011年5月22日－29日在美丽的青岛市举行了苏迪曼杯羽毛球混合团体锦标赛．在比赛中，某次羽毛球的运动路线可以看作是抛物线y＝－x2＋bx＋c的一部分(如下图)，其中出球点B离地面O点的距离是1 m，球落地点A到O点的距离是4 m，那么这条抛物线的解析式是

    [　　]
    A．

    y＝－x2＋x＋1

    B．

    y＝－x2＋x－1

    C．

    y＝－x2－x＋1

    D．

    y＝－x2－x－1

    查看答案和解析>>

    科目：初中数学 来源：2007年闵行区初三调研测试数学试卷 题型：044

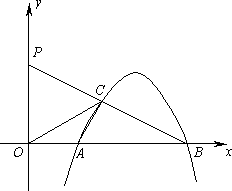
    　　如下图，抛物线y＝mx2－8mx－与x轴正半轴交于A(x1，0)、B(x2，0)两点，且x2＝3x1．

    (1)求m的值；

    (2)抛物线上另有一点C在第一象限，设BC的延长线交y轴于P．如果点C是BP的中点，求点C坐标；

    (3)在(2)的条件下，求证：△OCA∽△OBC．

    查看答案和解析>>

    科目：初中数学 来源：2009年湖南省益阳市中考数学试题 题型：044

    阅读材料：

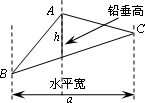
    如下图，过△ABC的三个顶点分别作出与水平线垂直的三条直线，外侧两条直线之间的距离叫△ABC的“水平宽”(a)，中间的这条直线在△ABC内部线段的长度叫△ABC的“铅垂高(h)”．我们可得出一种计算三角形面积的新方法：，即三角形面积等于水平宽与铅垂高乘积的一半．

    解答下列问题：

    如下图，抛物线顶点坐标为点C(1，4)，交x轴于点A(3，0)，交y轴于点B．

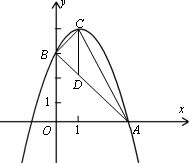
    (1)求抛物线和直线AB的解析式；

    (2)点P是抛物线(在第一象限内)上的一个动点，连结PA，PB，当P点运动到顶点C时，求△CAB的铅垂高CD及S△CAB；

    (3)是否存在一点P，使S△PAB＝S△CAB，若存在，求出P点的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源：2007年内蒙古自治区鄂尔多斯市初中毕业升学考试数学试题 题型：044

    如下图，抛物线y＝－x2＋2nx＋n2－9(n为常数)经过坐标原点和x轴上另一点C，顶点在第一象限．

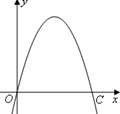
    (1)确定抛物线所对应的函数关系式，并写出顶点坐标；

    (2)在四边形OABC内有一矩形MNPQ，点M，N分别在OA，BC上，点Q，P在x轴上．当MN为多少时，矩形MNPQ的面积最大？最大面积是多少？

    查看答案和解析>>

    同步练习册答案