
分析 首先在△ACB的内部做∠ACD=25°,从而可得到△ADC为等腰三角形,然后再证明△BDC为等腰三角形,从而可得到问题的答案.
解答 解:如图所示:∠A=25°,∠B=80°,∠ACB=75°.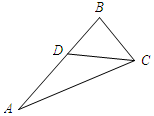
作∠ACD=∠A=25°,则三角形ADC为等腰三角形,且∠DCB=75°-25°=50°.
由三角形的外角的性质可知∠BDC=∠A+∠ACD=50°.
∴∠DCB=∠BDC,
∴△BDC为等腰三角形.
∴∠ADC=180°-50°=130°.
∴两个等腰三角形的顶角分别为130°、80°.
故答案为:130°、80°.
点评 本题主要考查的是等腰三角形的判定、三角形的外角的性质,熟练掌握相关知识是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 12π cm2 | B. | 15π cm2 | C. | 20π cm2 | D. | 25π cm2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知⊙O是四边形ABCD的外接圆,AB是⊙O的直径,BC=CD,过点C作PM⊥AD交AD的延长线于点M,交AB的延长线于点P.
如图,已知⊙O是四边形ABCD的外接圆,AB是⊙O的直径,BC=CD,过点C作PM⊥AD交AD的延长线于点M,交AB的延长线于点P.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源:2016-2017学年江苏省七年级下学期第一次月考数学试卷(解析版) 题型:解答题
已知如图,AB∥CD,试解决下列问题:
(1)∠1+∠2= ;
(2)∠1+∠2+∠3= ;
(3)∠1+∠2+∠3+∠4= ;
(4)试探究∠1+∠2+∠3+∠4+…+∠n= .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com