
分析 先根据已知的y代入计算求出f(2)、f(3)、f($\frac{1}{3}$),发现f(2)+f($\frac{1}{2}$)=$\frac{4}{5}$+$\frac{1}{5}$=1,f(3)+f($\frac{1}{3}$)=$\frac{9}{10}$+$\frac{1}{10}$=1,…,f(2016)+f($\frac{1}{2016}$)=1;一共有2015个1,由此可以得出结果.
解答 解:∵f(1)=$\frac{{1}^{2}}{1+{1}^{2}}$=$\frac{1}{2}$;
f(2)=$\frac{{2}^{2}}{1+{2}^{2}}$=$\frac{4}{5}$,f($\frac{1}{2}$)=$\frac{(\frac{1}{2})^{2}}{1+(\frac{1}{2})^{2}}$=$\frac{1}{5}$;
f(3)=$\frac{{3}^{2}}{1+{3}^{2}}$=$\frac{9}{10}$,f($\frac{1}{3}$)=$\frac{(\frac{1}{3})^{2}}{1+(\frac{1}{3})^{2}}$=$\frac{1}{10}$…
∴f(2)+f($\frac{1}{2}$)=$\frac{4}{5}$+$\frac{1}{5}$=1,f(3)+f($\frac{1}{3}$)=$\frac{9}{10}$+$\frac{1}{10}$=1,…,f(2016)+f($\frac{1}{2016}$)=1;
则f(1)+f(2)+f($\frac{1}{2}$)+f(3)+f($\frac{1}{3}$)+…+f(2016)+f($\frac{1}{2016}$),
=$\frac{1}{2}$+1+1+…+1,
=$\frac{1}{2}$+2015,
=2015.5,
故答案为:2015.5.
点评 本题既是求函数值问题,也是找规律问题,是数字类变化规律;此类题的解题思路为:根据已知所给式子,依次从1开始求值,并认真观察,总结规律,注意每个结果之间的关系;如果看不出来,尽量多计算几个函数值.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
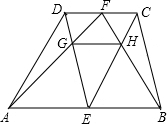 如图,梯形ABCD中,AB∥CD,AB=m,CD=n,E、F分别是AB、CD的中点,AF、ED相交于点G,BF、CE相交于点H,则GH=$\frac{mn}{m+n}$.
如图,梯形ABCD中,AB∥CD,AB=m,CD=n,E、F分别是AB、CD的中点,AF、ED相交于点G,BF、CE相交于点H,则GH=$\frac{mn}{m+n}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,AB是半圆的直径,点D是$\widehat{BC}$的中点,且AB=4,∠BAC=50°,则AD的长度为$\frac{13}{9}$πcm(结果保留π).
如图,AB是半圆的直径,点D是$\widehat{BC}$的中点,且AB=4,∠BAC=50°,则AD的长度为$\frac{13}{9}$πcm(结果保留π).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
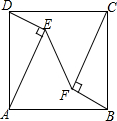 如图,在正方形ABCD中,分别以AD,BC为斜边作Rt△ADE和Rt△CBF,且Rt△ADE≌Rt△CBF,连结EF,若S正方形ABCD=20,S△ADE=3,则EF=4.
如图,在正方形ABCD中,分别以AD,BC为斜边作Rt△ADE和Rt△CBF,且Rt△ADE≌Rt△CBF,连结EF,若S正方形ABCD=20,S△ADE=3,则EF=4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com