
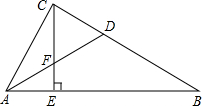
 如图,在Rt△ABC中,∠ACB=90°,AD平分∠BAC,交BC于点D,CE⊥AB,垂足为E,交AD于点F,试猜想△CFD的形状,证明你的结论.
如图,在Rt△ABC中,∠ACB=90°,AD平分∠BAC,交BC于点D,CE⊥AB,垂足为E,交AD于点F,试猜想△CFD的形状,证明你的结论.

科目:初中数学 来源: 题型:
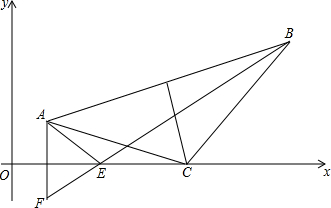 如图,x轴是西气东输工程天然气的主管道,按规定主管道在我市只允许开一个口,A(2,1),B(10,5)是我市新建的两个天然气站,现在要在x轴上选一个点开口,分别连接到A、B,小明说:“作AB的垂直平分线交x轴于C,就选点C,C点到A、B的距离相等.“小华说:“不行,可以用轴对称知识做出点E,点E到A、B的距离之和最小,这样可以节约原材料,节省费用.“请你求出:
如图,x轴是西气东输工程天然气的主管道,按规定主管道在我市只允许开一个口,A(2,1),B(10,5)是我市新建的两个天然气站,现在要在x轴上选一个点开口,分别连接到A、B,小明说:“作AB的垂直平分线交x轴于C,就选点C,C点到A、B的距离相等.“小华说:“不行,可以用轴对称知识做出点E,点E到A、B的距离之和最小,这样可以节约原材料,节省费用.“请你求出:查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com