
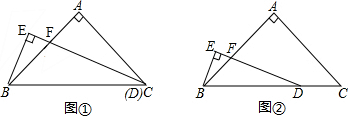
分析 (1)首先延长CA与BE交于点G,根据∠EDB=$\frac{1}{2}$∠C,BE⊥DE,判断出BE=EG=$\frac{1}{2}$BG;然后根据全等三角形的判定方法,判断出△ABG≌△ACF,即可判断出BG=CF=FD,再根据BE=$\frac{1}{2}$BG,可得BE=$\frac{1}{2}$FD,据此判断即可.
(2)首先过点D作DG∥AC,与AB交于H,与BE的延长线交于G,根据DG∥AC,∠BAC=90°,判断出∠BDE=∠EDG;然后根据全等三角形的判定方法,判断出△DEB≌△DEG,即可判断出BE=EG=$\frac{1}{2}$BG;最后根据全等三角形的判定方法,判断出△BGH≌△DFH,即可判断出BG=FD,所以BE=$\frac{1}{2}$FD,据此判断即可.
解答 解:(1)如图①,延长CA与BE交于点G,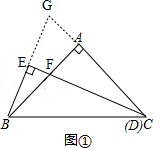 ,
,
∵∠EDB=$\frac{1}{2}$∠C,
∴∠EDG=∠BDG-∠BDE=∠C-$\frac{1}{2}$∠C=$\frac{1}{2}$∠C,
∴∠BDE=∠EDG,
即CE是∠BCG的平分线,
又∵BE⊥DE,
∴BE=EG=$\frac{1}{2}$BG,
∵∠BED=∠BAD=90°,∠BFE=∠CFA,
∴∠EBF=∠ACF,
即∠ABG=∠ACF,
在△ABG和△ACF中,
$\left\{\begin{array}{l}{∠ABG=∠ACF}\\{AB=AC}\\{∠BAG=∠CAF=90°}\end{array}\right.$
∴△ABG≌△ACF,
∴BG=CF=FD,
又∵BE=$\frac{1}{2}$BG,
∴BE=$\frac{1}{2}$FD.
(2)如图②,过点D作DG∥AC,与AB交于H,与BE的延长线交于G,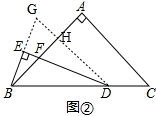 ,
,
∵DG∥AC,∠BAC=90°,
∴∠BDG=∠C,∠BHD=∠BHG=∠BAC=90°,
又∵∠BDE=$\frac{1}{2}$∠C,
∴∠EDG=∠BDG-∠BDE=∠C-$\frac{1}{2}$∠C=$\frac{1}{2}$∠C,
∴∠BDE=∠EDG,
在△DEB和△DEG中,
$\left\{\begin{array}{l}{∠BDE=∠EDG}\\{DE=DE}\\{∠DEB=∠DEG=90°}\end{array}\right.$
∴△DEB≌△DEG,
∴BE=EG=$\frac{1}{2}$BG,
∵AB=AC,∠BAC=90°,
∴∠ABC=∠ACB=∠GDB,
∴HB=HD,
∵∠BED=∠BHD=90°,∠BFE=∠DFH,
∴∠EBF=∠HDF,
即∠HBG=∠HDF,
在△BGH和△DFH中,
$\left\{\begin{array}{l}{∠HBG=∠HDF}\\{HB=HD}\\{∠BHG=∠DHF}\end{array}\right.$
∴△BGH≌△DFH,
∴BG=FD,
又∵BE=$\frac{1}{2}$BG,
∴BE=$\frac{1}{2}$FD,
即①中的结论还成立.
点评 (1)此题主要考查了全等三角形的判定和性质的应用,要熟练掌握,解答此题的关键是要明确:①在判定三角形全等时,关键是选择恰当的判定条件.②在应用全等三角形的判定时,要注意三角形间的公共边和公共角,必要时添加适当辅助线构造三角形.
(2)此题还考查了等腰直角三角形的性质和应用,要熟练掌握,解答此题的关键是要明确:等腰直角三角形是一种特殊的三角形,具有所有三角形的性质,还具备等腰三角形和直角三角形的所有性质,即:两个锐角都是45°,斜边上中线、角平分线、斜边上的高,三线合一,等腰直角三角形斜边上的高为外接圆的半径R,而高又为内切圆的直径.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
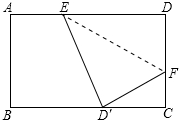 如图将矩形ABCD纸片沿EF折叠,使D点与BC边的中点D′重合,若BC=8,CD=6,则CF=( )
如图将矩形ABCD纸片沿EF折叠,使D点与BC边的中点D′重合,若BC=8,CD=6,则CF=( )| A. | $\frac{5}{3}$ | B. | $\frac{3}{5}$ | C. | $\frac{4}{5}$ | D. | $\frac{5}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
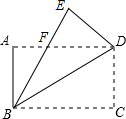 如图,四边形ABCD是矩形,把矩形沿对角线BD折叠,点C落在点E处,BE与AD相交于点E.
如图,四边形ABCD是矩形,把矩形沿对角线BD折叠,点C落在点E处,BE与AD相交于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,矩形ABCD中,AB=8cm,BC=6cm,动点P从点A出发,以每秒1cm的速度沿线段AB向点B运动,连接DP,把∠A沿DP折叠,使点A落在点A′处.求出当△BPA′为直角三角形时,点P运动的时间.
如图,矩形ABCD中,AB=8cm,BC=6cm,动点P从点A出发,以每秒1cm的速度沿线段AB向点B运动,连接DP,把∠A沿DP折叠,使点A落在点A′处.求出当△BPA′为直角三角形时,点P运动的时间.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com