
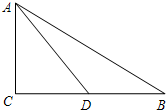
 已知:如图,在Rt△ABC中,∠C=90°,AC=CD,∠B=30°,AD=2$\sqrt{2}$.
已知:如图,在Rt△ABC中,∠C=90°,AC=CD,∠B=30°,AD=2$\sqrt{2}$.分析 由等腰直角三角形的性质得出AC=CD=$\frac{\sqrt{2}}{2}$AD=2,由含30°角的直角三角形的性质得出AB=2AC=4,由勾股定理求出BC,即可得出DB的长.
解答 解:∵∠C=90°,AC=CD,
∴△ACD是等腰直角三角形,
∴AC=CD=$\frac{\sqrt{2}}{2}$AD=$\frac{\sqrt{2}}{2}$×2$\sqrt{2}$=2,
又∵∠B=30°,
∴AB=2AC=4.
∴BC=$\sqrt{A{B}^{2}-A{C}^{2}}$=2$\sqrt{3}$,
∴DB=BC-CD=2$\sqrt{3}$-2.
点评 本题考查了勾股定理、含30°角的直角三角形的性质、等腰直角三角形的性质,熟练掌握勾股定理,由勾股定理求出AC、BC是解决问题的关键.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:选择题
| A. | a≥-3 | B. | a>-3 | C. | a≤-3 | D. | a<-3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ${(\frac{2}{3})^2}=\frac{9}{2}$ | B. | ${(-\frac{3}{2})^3}=-\frac{27}{2}$ | C. | ${(-\frac{3}{2})^2}=-\frac{9}{4}$ | D. | ${(-\frac{3}{2})^3}=-\frac{27}{8}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com