
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
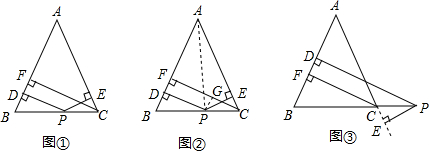
| 13 |
| 37 |
查看答案和解析>>
科目:初中数学 来源: 题型:
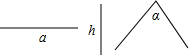 已知三角形的一边a,垂直于a的高h,以及a的对角α,你认为只利用尺规作图能作出这个三角形吗?
已知三角形的一边a,垂直于a的高h,以及a的对角α,你认为只利用尺规作图能作出这个三角形吗?查看答案和解析>>
科目:初中数学 来源: 题型:
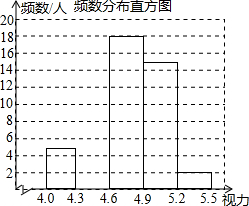 为了了解学生的视力情况,某中学对该校学生进行一次视力抽样调查,根据抽样调查的情况,绘制成如下统计图表(不完整):
为了了解学生的视力情况,某中学对该校学生进行一次视力抽样调查,根据抽样调查的情况,绘制成如下统计图表(不完整):| 组别 | 分组 | 频数(人) | 频率 |
| A | 4.0≤x<4.3 | 5 | 0.1 |
| B | 4.3≤x<4.6 | 0.2 | |
| C | 4.6≤x<4.9 | 18 | 0.36 |
| D | 4.9≤x<5.2 | 15 | |
| E | 5.2≤x<5.5 | 2 | 0.04 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com