
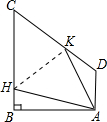
 已知直角梯形ABCD中,∠DAB=∠B=90°,AD=4,DC=BC=8,将四边形ABCD折叠,使A与C重合,HK为折痕,则CH=________,AK=________.
已知直角梯形ABCD中,∠DAB=∠B=90°,AD=4,DC=BC=8,将四边形ABCD折叠,使A与C重合,HK为折痕,则CH=________,AK=________. y,再表示出AK、AF,然后在Rt△AKF中,利用勾股定理列式计算即可求出y,从而得解.
y,再表示出AK、AF,然后在Rt△AKF中,利用勾股定理列式计算即可求出y,从而得解. =
= =4
=4 ,
, ,
,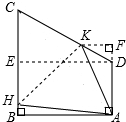
 )2+(8-x)2=x2,
)2+(8-x)2=x2, KD=y,KF=
KD=y,KF=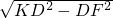 =
=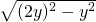 =
= y,
y, y)2=(8-2y)2,
y)2=(8-2y)2,

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
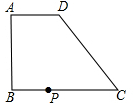 PD中边AP上的高为( )
PD中边AP上的高为( )A、
| ||||
B、
| ||||
C、
| ||||
| D、3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 | 2 |
 结论是否成立?请说明理由.
结论是否成立?请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:
 已知直角梯形ABCD如图放置在平面直角坐标系中,∠DCB=30°,AB边在y轴上,点D的横坐标为6,CQ⊥x轴,垂足为Q,点Q的横坐标为12,过CD的直线l交x轴于点E,E点坐标为(18,0).
已知直角梯形ABCD如图放置在平面直角坐标系中,∠DCB=30°,AB边在y轴上,点D的横坐标为6,CQ⊥x轴,垂足为Q,点Q的横坐标为12,过CD的直线l交x轴于点E,E点坐标为(18,0).查看答案和解析>>
科目:初中数学 来源: 题型:
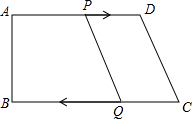 C同时出发,当其中一点到达端点时,另一点也随之停止运动,设运动时间为t.
C同时出发,当其中一点到达端点时,另一点也随之停止运动,设运动时间为t.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com