
κ��ʱ�ڵ���ѧ�������״���Բ����Ϊ����Բ���ʽ��������ܵ����ۺ����Ƶ��㷨����Բ�ڽ�������Σ���������εı�����������ʱ�����ܳ������ӽ�Բ���ܳ����������� ����ý�Ϊ��ȷ��Բ���ʣ����֮�����յĻ����ϼ���Ŭ������������εı�������24576ʱ���õ��˾�ȷ��С�������λ��Բ���ʣ���һ�ɾ��ڵ�ʱ��������������һǧ���꣬��ͼ�����ݡ���Բ��������Բ�ڽ�����������õ�Բ���ʵĽ���ֵ�ǣ�������
����ý�Ϊ��ȷ��Բ���ʣ����֮�����յĻ����ϼ���Ŭ������������εı�������24576ʱ���õ��˾�ȷ��С�������λ��Բ���ʣ���һ�ɾ��ڵ�ʱ��������������һǧ���꣬��ͼ�����ݡ���Բ��������Բ�ڽ�����������õ�Բ���ʵĽ���ֵ�ǣ�������

A. 0.5 B. 1 C. 3 D. ��

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��������2019����꼶���ϣ�������ѧģ���� ���ͣ���ѡ��
���κ���y=x2+2�Ķ��������ǣ�������
A. ��1����2�� B. ��1��2�� C. ��0����2�� D. ��0��2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���˽̰����꼶��ѧ�ϲ�_��һ��_������_��Ԫ����Ծ� ���ͣ������
��һ��



�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ɽ��ʡ̫ԭ��2018���п���ѧһģ�Ծ� ���ͣ������
��ͼ��AB�ǡ�O��ֱ������DE��AB�ڵ�F����O������BC��AD���ӳ��߽��ڵ�C������AE��
��1�����жϡ�AED���C��������ϵ����˵�����ɣ�
��2����AD=3����C=60�㣬��E�ǰ�ԲAB���е㣬���߶�AE�ij�Ϊ�� ����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ɽ��ʡ̫ԭ��2018���п���ѧһģ�Ծ� ���ͣ������
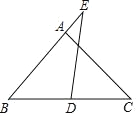
��ͼ����Rt��ABC�У���BAC=90�㣬AB=AC=4��D��BC���е㣬��E��BA���ӳ����ϣ�����ED����AE=2����DE�ij�Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ɽ��ʡ̫ԭ��2018���п���ѧһģ�Ծ� ���ͣ���ѡ��
������������y=3x��ͼ��A����2��y1����B����1��y2�����㣬��y1��y2�Ĵ�С��ϵΪ��������
A. y1��y2 B. y1��y2 C. y1��y2 D. y1��y2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ����ʦ���2019���һѧ�ھ��꼶��ѧ_�ϲ�_��һ��_����ƽ���ı���_��Ԫ����Ծ�_ ���ͣ������
��ͼ����֪



















�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ����ʦ���2019���һѧ�ھ��꼶��ѧ_�ϲ�_��һ��_����ƽ���ı���_��Ԫ����Ծ�_ ���ͣ���ѡ��
��ͼ���ı���

 ��
��




A. 



�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2019�컪ʦ�����꼶��ѧ�ϲ��ۺϼ���Ծ�����21-23�£� ���ͣ������
��ƽ��ֱ������ϵ�У���

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com