【题目】“保护环境,人人有责”，为了更好的利用水资源,某污水处理厂决定购买
、
两型号污水处理设备共10台,其信息如下表.(1)设购买型设备
台,所需资金共为
万元,每月处理污水总量为
吨,试写出与之间的函数关系式,与之间的函数关系式；(2)经预算,该污水处理厂购买设备的资金不超过88万元, 每月处理污水总量不低于2080吨,请你列举出所有购买方案,并指出哪种方案最省钱,需多少资金？
第三学期赢在暑假系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案科目：初中数学 来源： 题型：
【题目】如图，在ABCD中，E为边CD上一点，将△ADE沿AE折叠至△AD′E处，AD′与CE交于点F．若∠B=52°，∠DAE=20°，则∠FED′的大小为 ．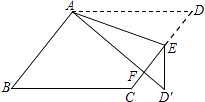 
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图A在数轴上所对应的数为﹣2．
（1）点B在点A右边距A点4个单位长度，求点B所对应的数；
（2）在（1）的条件下，点A以每秒2个单位长度沿数轴向左运动，点 B 以每秒2个单位长度沿数轴向右运动，当点A运动到﹣6所在的点处时，求A，B两点间距离．
（3）在（2）的条件下，现A点静止不动，B点再以每秒2个单位长度沿数轴向左运动时，经过多长时间A，B两点相距4个单位长度．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某单位在五月份准备组织部分员工到北京旅游，现联系了甲、乙两家旅行社，两家旅行社报价均为3000元/人，两家旅行社同时都对10人以上的团体推出了优惠举措；甲旅行社对每位员工七五折优惠，而乙旅行社是免去一位带队管理员工的费用，其余员工八折优惠．
（1）如果设参加旅游的员工共有a（a＞10人），则甲旅行社的费用为 元，乙旅行社的费用为 元；（用含a的代数式表示，并化简）
（2）如果计划在五月份外出旅游七天，设最中间一天的日期为x，则这七天的日期之和为 ．（用含x的代数式表示，并化简）
（3）在（2）的条件下，假如这七天的日期之和为49的倍数，则他们可能于五月几号出发？（写出所有符合条件的可能性，并写出简单的计算过程）
（4）假如这个单位现组织包括管理员工在内的共20名员工到北京旅游，该单位选择哪一家旅行社比较优惠？请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图(甲)，在正方形
中，
是
上一点，
是
延长线上一点，且
．
(1)求证:
；
(2)在如图(甲)中，若
在上，且
，则
成立吗？
证明你的结论．(3)运用(1)(2)解答中积累的经验和知识，完成下题:
如图(乙)四边形中，∥
(＞)，
，
,点是上一点，且
，
，求
的长．
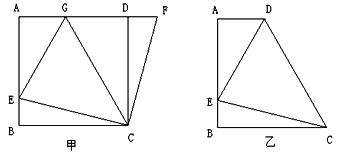
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，以△ABC的三边为边分别作等边△ACD、△ABE、△BCF， 则下列结论：
①△EBF≌△DFC；
②四边形AEFD为平行四边形；
③当AB=AC，∠BAC=1200时，四边形AEFD是正方形．
其中正确的结论是 ．（请写出正确结论的番号）．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在正方形ABCD中，点E在边AD上，点F在边BC的延长线上，连结EF与边CD相交于点G，连结BE与对角线AC相交于点H，AE=CF，BE=EG．
（1）求证：EF∥AC；
（2）求∠BEF大小；
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】探究多边形内角和问题．
连接多边形不相邻的两个顶点的线段叫做多边形的对角线．从多边形某一个顶点出发的×对角线可以把一个多边形分成几个三角形．这样就把多边形内角和问题转化为三角形内角和问题了．
（1）请你试一试，做一做，把下面表格补充完整：
名称 | 图形 | 内角和 |
三角形 |
| 180° |
四边形 |
| 2×180°=360° |
五边形 |
|
|
六边形 |
|
|
… | … | … |
根据表格探究发现的规律，完成下面的问题：
（2）七边形的内角和等于 度；
（3）如果一个多边形有n条边，请你用含有n的代数式表示这个多边形的内角和： ．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
