
【题目】如图,在正方形ABCD中,点E在边AD上,点F在边BC的延长线上,连结EF与边CD相交于点G,连结BE与对角线AC相交于点H,AE=CF,BE=EG.

(1)求证:EF∥AC;
(2)求∠BEF大小;
【答案】(1)、证明过程见解析;(2)、60°.
【解析】试题分析:(1)、根据正方形的性质得出AD∥BF,结合AE=CF可得四边形ACFE是平行四边形,从而得出EF∥AC;(2)、连接BG,根据EF∥AC可得∠F=∠ACB=45°,根据∠GCF=90°可得∠CGF=∠F=45°可得CG=CF,根据AE=CF可得AE=CG,从而得出△BAE≌△BCG,即BE=EG,得出△BEG为等边三角形,得出∠BEF的度数.
试题解析:(1)、∵四边形ABCD是正方形 ∴AD∥BF ∵AE="CF" ∴四边形ACFE是平行四边形 ∴EF∥AC
(2)、连接BG ∵EF∥AC, ∴∠F=∠ACB=45°, ∵∠GCF=90°, ∴∠CGF=∠F=45°, ∴CG=CF,
∵AE=CF, ∴AE=CG, ∴△BAE≌△BCG(SAS) ∴BE=BG, ∵BE=EG, ∴△BEG是等边三角形,
∴∠BEF=60°


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:初中数学 来源: 题型:
【题目】已知小华家、小夏家、小红家及学校在同一条大路旁,一天,他们放学后从学校出发,先向南行1000m到达小华家A处,继续向北行3000m到达小红B家处,然后向南行6000m到小夏家C处.
(1)以学校以原点,以向南方向为正方向,用1个单位长度表示1000m,请你在数轴上表示出小华家、小夏家、小红家的位置;
(2)小红家在学校什么位置?离学校有多远?
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“保护环境,人人有责”,为了更好的利用水资源,某污水处理厂决定购买![]() 、
、![]() 两型号污水处理设备共10台,其信息如下表.(1)设购买
两型号污水处理设备共10台,其信息如下表.(1)设购买![]() 型设备
型设备![]() 台,所需资金共为
台,所需资金共为![]() 万元,每月处理污水总量为
万元,每月处理污水总量为![]() 吨,试写出
吨,试写出![]() 与
与![]() 之间的函数关系式,
之间的函数关系式,![]() 与
与![]() 之间的函数关系式;(2)经预算,该污水处理厂购买设备的资金不超过88万元, 每月处理污水总量不低于2080吨,请你列举出所有购买方案,并指出哪种方案最省钱,需多少资金?
之间的函数关系式;(2)经预算,该污水处理厂购买设备的资金不超过88万元, 每月处理污水总量不低于2080吨,请你列举出所有购买方案,并指出哪种方案最省钱,需多少资金?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小亮从家步行到公交车站台,等公交车去学校. 图中的折线表示小亮的行程s(km)与所花时间t(min)之间的函数关系. 下列说法错误的是

A. 他离家8km共用了30min B. 他等公交车时间为6min
C. 他步行的速度是100m/min D. 公交车的速度是350m/min
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】水果批发市场有一种高档水果,如果每千克盈利(毛利润)10元,每天可售出500千克,经市场调查发现,在进货价不变的情况下,若每千克涨价1元,日销量将减少20千克.
(1)若以每千克能盈利18元的单价出售,问每天的总毛利润为多少元?
(2)现市场要保证每天总毛利润6000元,同时又要使顾客得到实惠,则每千克应涨价多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,网格线的交点叫格点,格点![]() 是
是![]() 的边
的边![]() 上的一点(请利用网格作图,保留作图痕迹).
上的一点(请利用网格作图,保留作图痕迹).

(1)过点![]() 画
画![]() 的垂线,交
的垂线,交![]() 于点
于点![]() ;
;
(2)线段 的长度是点O到PC的距离;
(3)![]() 的理由是 ;
的理由是 ;
(4)过点C画![]() 的平行线;
的平行线;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ABC=90°,点D,F分别是AC,AB的中点,CE∥DB,BE∥DC.
(1)求证:四边形DBEC是菱形;
(2)若AD=3,DF=1,求四边形DBEC面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y1=kx+b与双曲线y2= ![]() 交于A、B两点,它们的横坐标分别为1和5.
交于A、B两点,它们的横坐标分别为1和5. 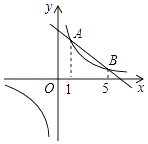
(1)当m=5时,求直线AB的解析式及△AOB的面积;
(2)当y1>y2时,直接写出x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=50°,把△ABC沿EF折叠,C对应点恰好与△ABC的外心O重合,则∠CFE的度数是( ) 
A.40°
B.45°
C.50°
D.55°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com