
【题目】如图,在Rt ![]() 中,∠A=90°,点O在AC上,⊙O切BC于点E,A在⊙O上,若AB=5,AC=12,求⊙O的半径.
中,∠A=90°,点O在AC上,⊙O切BC于点E,A在⊙O上,若AB=5,AC=12,求⊙O的半径.
科目:初中数学 来源: 题型:
【题目】如图,已知∠AOB=90![]() ,射线OC绕点O从OA位置开始,以每秒4
,射线OC绕点O从OA位置开始,以每秒4![]() 的速度顺时针方向旋转;同时,射线OD绕点O从OB位置开始,以每秒1
的速度顺时针方向旋转;同时,射线OD绕点O从OB位置开始,以每秒1![]() 的速度逆时针方向旋转. 当OC与OA成180
的速度逆时针方向旋转. 当OC与OA成180![]() 时,OC与OD同时停止旋转.
时,OC与OD同时停止旋转.
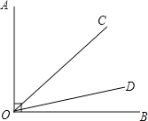
(1)当OC旋转10秒时,∠COD=___.
(2)当OC与OD的夹角是30![]() 时,求旋转的时间.
时,求旋转的时间.
(3)当OB平分∠COD时,求旋转的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
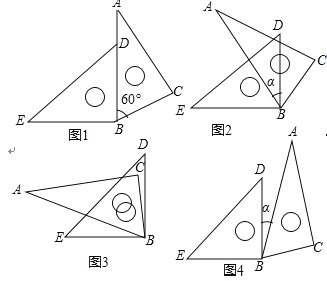
【题目】图1是由一副三角板拼成的图案,其中![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)求图1中![]() 的度数;
的度数;
(2)若将图1中的三角板![]() 不动,将另一三角板
不动,将另一三角板![]() 绕点
绕点![]() 顺时针或逆时针旋转
顺时针或逆时针旋转![]() 度(
度(![]() ).当
).当![]() 时,求
时,求![]() 的度数(图2,图3,图4仅供参考).
的度数(图2,图3,图4仅供参考).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若a、b、c是正数,下列各式,从左到右的变形不能用如图验证的是( )
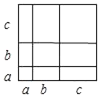
A. (b+c)2=b2+2bc+c2
B. a(b+c)=ab+ac
C. (a+b+c)2=a2+b2+c2+2ab+2bc+2ac
D. a2+2ab=a(a+2b)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知直线y=﹣![]() x+4与x轴、y轴分别交于A、B两点,点C(0,n)是y轴上一点.把坐标平面沿直线AC折叠,使点B刚好落在x轴上,则点C的坐标为______.
x+4与x轴、y轴分别交于A、B两点,点C(0,n)是y轴上一点.把坐标平面沿直线AC折叠,使点B刚好落在x轴上,则点C的坐标为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年元旦期间,某超市打出促销广告,如下表所示:
一次性所购物品的原价 | 优惠办法 |
不超过200元 | 没有优惠 |
超过200元,但不超过600元 | 全部按九折优惠 |
超过600元 | 其中600元仍按九折优惠,超过600元部分按8折优惠 |
(1)小张一次性购买物品的原价为400元,则实际付款为 元;
(2)小王购物时一次性付款580元,则所购物品的原价是多少元?
(3)小赵和小李分别前往该超市购物,两人各自所购物品的原价之和为1200元,且小李所购物品的原价高于小赵,两人实际付款共1074元,则小赵和小李各自所购物品的原价分别是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CD∥AB,OE平分∠AOD,OF⊥OE,OG⊥CD,∠CDO=50°,则下列结论:
① ∠AOE=65°;② OF平分∠BOD;③ ∠GOE=∠DOF;④ ∠AOE=∠GOD,其中正确结论的个数是( )

A. 4个B. 3个C. 2个D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了丰富学生的校园生活,准备购进一批篮球和足球.其中篮球的单价比足球的单价多40元,用1500元购进的篮球个数与900元购进的足球个数相等.
(1)篮球和足球的单价各是多少元?
(2)该校打算用1000元购买篮球和足球,问恰好用完1000元,并且篮球、足球都买有的购买方案有哪几种?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com