
【题目】2019年元旦期间,某超市打出促销广告,如下表所示:
一次性所购物品的原价 | 优惠办法 |
不超过200元 | 没有优惠 |
超过200元,但不超过600元 | 全部按九折优惠 |
超过600元 | 其中600元仍按九折优惠,超过600元部分按8折优惠 |
(1)小张一次性购买物品的原价为400元,则实际付款为 元;
(2)小王购物时一次性付款580元,则所购物品的原价是多少元?
(3)小赵和小李分别前往该超市购物,两人各自所购物品的原价之和为1200元,且小李所购物品的原价高于小赵,两人实际付款共1074元,则小赵和小李各自所购物品的原价分别是多少元?
【答案】(1)360;(2)650;(3)540,660.
【解析】
(1)因为小张一次性购买物品的原价为400元,应按九折付款,计算即可得出答案;
(2)因为小王购物时一次性付款580元,所以原价超过600元,按超过600元的优惠办法计算即可得出答案;
(3)因为两人各自所购物品的原价之和为1200元,且小李所购物品的原价高于小赵,所以小赵所购物品的原价少于600元,设小赵所购商品的价格是x元,分x![]() 200和x>200两种情况,列出方程解出即可.
200和x>200两种情况,列出方程解出即可.
解:
(1)400×0.9=360;
(2)600×0.9=540(元),580-540=40(元),40÷0.8=50(元);600+50=650(元)
(3)设小赵所购商品的价格是x元,
①若x![]() 200,x+540+0.8(1200-x-600)=1074 解得:x=270(舍去)
200,x+540+0.8(1200-x-600)=1074 解得:x=270(舍去)
②若x>200,0.9x+540+0.8(1200-x-600)=1074 解得:x=540 1200-540=660(元);
综上所述,小赵和小李各自所购物品的原价分别是540元和660元.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】我们知道,对于一个图形,通过两种不同的方法计算它的面积,可以得到一个数学等式.例如构造图1可以得到![]() .请解答下列问题:
.请解答下列问题:
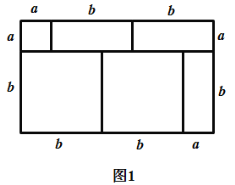
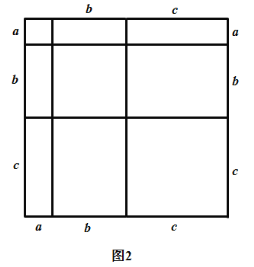
(1)仿照图1,构造适当的图形得到![]() 的值;
的值;
(2)写出图2中所表示的数学等式;
(3)利用(2)中所得到的结论,解决下面的问题:己知![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,AB=AC,D为边BC上一点,以AB,BD为邻边作平行四边形ABDE,连接AD,EC.
(1)求证:△ADC≌△ECD;
(2)当点D在什么位置时,四边形ADCE是矩形,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发.设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系.根据题中所给信息解答以下问题:
(1)甲、乙两地之间的距离为____km;图中点C的实际意义为:______;慢车的速度为_______,快车的速度为______;
(2)求线段BC所表示的y与x之间的函数关系式,以及自变量x的取值范围;
(3)若在第一列快车与慢车相遇时,第二列快车从乙地出发驶往甲地,速度与第一列快车相同.请直接写出第二列快车出发多长时间,与慢车相距200km.
(4)若第三列快车也从乙地出发驶往甲地,速度与第一列快车相同.如果第三列快车不能比慢车晚到,求第三列快车比慢车最多晚出发多少小时?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一条东西走向河的一侧有一村庄C,河边原有两个取水点A,B,其中AB=AC,由于某种原因,由C到A的路现在已经不通,某村为方便村民取水决定在河边新建一个取水点H(A、H、B在一条直线上),并新修一条路CH,测得CB=3千米,CH=2.4千米,HB=1.8千米.
(1)问CH是否为从村庄C到河边的最近路?(即问:CH与AB是否垂直?)请通过计算加以说明;
(2)求原来的路线AC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 特例研究:如图
特例研究:如图![]() ,等边
,等边![]() 的边长为8,求等边
的边长为8,求等边![]() 的高.
的高.
![]() 经验提升:
经验提升:
如图![]() ,在
,在![]() 中,
中,![]() ,点P为射线BC上的任一点,过点P作
,点P为射线BC上的任一点,过点P作![]() ,
,![]() ,垂足分别为D、E,过点C作
,垂足分别为D、E,过点C作![]() ,垂足为
,垂足为![]() 补全图形,判断线段PD,PE,CF的数量关系,并说明理由.
补全图形,判断线段PD,PE,CF的数量关系,并说明理由.
![]() 综合应用:
综合应用:
如图![]() ,在平面直角坐标系中有两条直线
,在平面直角坐标系中有两条直线![]() :
:![]() ,
,![]() :
:![]() ,若线段BC上有一点M到
,若线段BC上有一点M到![]() 的距离是1,请运用
的距离是1,请运用![]() 中的结论求出点M的坐标.
中的结论求出点M的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,山坡上有一棵树AB,树底部B点到山脚C点的距离BC为6![]() 米,山坡的坡角为30°. 小宁在山脚的平地F处测量这棵树的高,点C到测角仪EF的水平距离CF = 1米,从E处测得树顶部A的仰角为45°,树底部B的仰角为20°(结果精确到0.1).
米,山坡的坡角为30°. 小宁在山脚的平地F处测量这棵树的高,点C到测角仪EF的水平距离CF = 1米,从E处测得树顶部A的仰角为45°,树底部B的仰角为20°(结果精确到0.1).
(1)求树AB与测角仪EF的水平距离DF的长;
(2)求树AB的高度.(参考数值:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36, ![]() ≈1.73 )
≈1.73 )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小晗家客厅里装有一种三位单极开关,分别控制着A(楼梯)、B(客厅)、C(走廊)三盏电灯,在正常情况下,小晗按下任意一个开关均可打开对应的一盏电灯,既可三盏、两盏齐开,也可分别单盏开.因刚搬进新房不久,不熟悉情况.
(1)若小晗任意按下一个开关,正好楼梯灯亮的概率是多少?
(2)若任意按下一个开关后,再按下另两个开关中的一个,则正好客厅灯和走廊灯同时亮的概率是多少?请用树状图法或列表法加以说明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com