(1)证明:如图D2-2,连结OD.
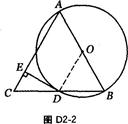
∵OA=OB,CD=BD,∴OD∥AC.
∴∠0DE=∠CED.
又∵DE⊥AC,∴∠CED=90°.∴∠ODE=90°,即OD⊥DE.
∴DE是⊙O的切线.
(2)解:∵OD∥AC,∠BAC=60°,∴∠BOD=∠BAC=60°,
∠C=∠0DB.
又∵OB=OD,∴△BOD是等边三角形.
∴∠C=∠ODB=60°,CD=BD=5.
∵DE⊥AC,∴DE=CD·sin∠C =5×sin60°=
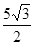
.
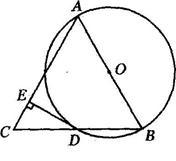
(1)连接OD,根据OA=OB,CD=BD,得出OD∥AC,∠0DE=∠CED,再根据DE⊥AC,即可证出OD⊥DE,从而得出答案;
(2)结合(1)中的结论,可以证明△BOD是等边三角形,即可求得CD和BD的长,再根据锐角三角函数即可计算DE的长.

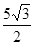

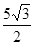 .
. 

 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案