
 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:初中数学 来源: 题型:
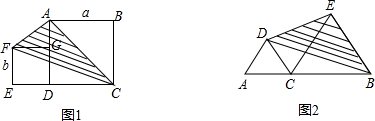 在数学学习过程中,我们常常会有“似曾相识“的感觉,如果我们把这些类似进行比较、加以联想的话,可能出现许多意想不到的结果和方法,这种把类似进行比较、联想,从而解决问题的方法就是类比法,类比法是一种寻求解题思路,猜测问题答案或结论的发现方法.
在数学学习过程中,我们常常会有“似曾相识“的感觉,如果我们把这些类似进行比较、加以联想的话,可能出现许多意想不到的结果和方法,这种把类似进行比较、联想,从而解决问题的方法就是类比法,类比法是一种寻求解题思路,猜测问题答案或结论的发现方法.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com