
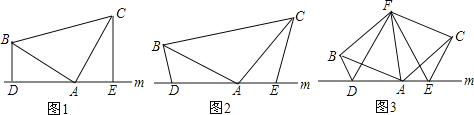
【题目】(1)如图1,已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E.猜测DE、BD、CE三条线段之间的数量关系(直接写出结果即可).
(2)如图2,将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请问第(1)题中DE、BD、CE之间的关系是否仍然成立?如成立,请你给出证明;若不成立,请说明理由.
(3)拓展与应用:如图3,D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,试判断线段DF、EF的数量关系,并说明理由.
【答案】(1) DE=BD+CE;(2)DE=BD+CE的关系仍然成立.理由见解析;(3) DF=EF.理由见解析.
【解析】
(1)利用已知得出∠CAE=∠ABD,进而利用AAS得出则△ABD≌△CAE,即可得出DE=BD+CE;
(2)根据∠BDA=∠AEC=∠BAC=α,得出∠CAE=∠ABD,在△ADB和△CEA中,根据AAS证出△ADB≌△CEA,从而得出AE=BD,AD=CE,即可证出DE=BD+CE;
(3)与前面的结论得到△ADB≌△CEA,则BD=AE,∠DBA=∠CAE,根据等边三角形的性质得∠ABF=∠CAF=60°,则∠DBA+∠ABF=∠CAE+∠CAF,则∠DBF=∠FAE,利用“SAS”可判断△DBF≌△EAF,所以DF=EF.
解:(1)DE、BD、CE三条线段之间的数量关系是DE=BD+CE.理由如下: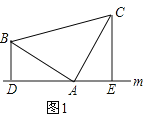
如图1,∵BD⊥m,CE⊥m,
∴∠BDA=∠AEC=90°
又∵∠BAC=90°,
∴∠BAD+∠CAE=90°,∠BAD+∠ABD=90°,
∴∠CAE=∠ABD
在△ABD和△CAE中,
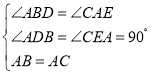
∴△ABD≌△CAE(AAS)
∴BD=AE,AD=CE,
∵DE=AD+AE,
∴DE=CE+BD;
(2)如图2,

∵∠BDA=∠AEC=∠BAC=α,
∴∠DBA+∠BAD=∠BAD+∠CAE=180°-α,
∴∠CAE=∠ABD,
在△ADB和△CEA中
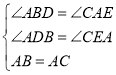
∴△ADB≌△CEA(AAS),
∴AE=BD,AD=CE,
∴BD+CE=AE+AD=DE;
(3)DF=EF.理由如下:
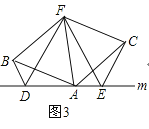
由(2)知,△ADB≌△CAE,
BD=EA,∠DBA=∠CAE,
∵△ABF和△ACF均为等边三角形,
∴∠ABF=∠CAF=60°,BF=AF
∴∠DBA+∠ABF=∠CAE+∠CAF,
∴∠DBF=∠FAE,
在△DBF和△EAF中,
∴△DBF≌△EAF(SAS),
∴DF=EF.


 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,将矩形MNPQ放置在矩形ABCD中,使点M,N分别在AB,AD边上滑动,若MN=6,PN=4,在滑动过程中,点A与点P的距离AP的最大值为( )
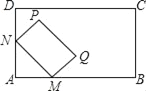
A. 4 B. 2![]() C. 7 D. 8
C. 7 D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:BD为![]() 的直径,O为圆心,点A为圆上一点,过点B作
的直径,O为圆心,点A为圆上一点,过点B作![]() 的切线交DA的延长线于点F,点C为
的切线交DA的延长线于点F,点C为![]() 上一点,且
上一点,且![]() ,连接BC交AD于点E,连接AC.
,连接BC交AD于点E,连接AC.
![]() 如图1,求证:
如图1,求证:![]() ;
;
![]() 如图2,点H为
如图2,点H为![]() 内部一点,连接OH,CH若
内部一点,连接OH,CH若![]() 时,求证:
时,求证:![]() ;
;
![]() 在
在![]() 的条件下,若
的条件下,若![]() ,
,![]() 的半径为10,求CE的长.
的半径为10,求CE的长.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】濠河成功晋升国家![]() 级旅游景区,为了保护这条美丽的护城河,南通市政府投入大量资金治理濠河污染,在城郊建立了一个大型污水处理厂,设库池中有待处理的污水
级旅游景区,为了保护这条美丽的护城河,南通市政府投入大量资金治理濠河污染,在城郊建立了一个大型污水处理厂,设库池中有待处理的污水![]() 吨,又从城区流入库池的污水按每小时
吨,又从城区流入库池的污水按每小时![]() 吨的固定流量增加,如果同时开动
吨的固定流量增加,如果同时开动![]() 台机组需
台机组需![]() 小时刚好处理完污水,同时开动
小时刚好处理完污水,同时开动![]() 台机组需
台机组需![]() 小时刚好处理完污水,若需要
小时刚好处理完污水,若需要![]() 小时内将污水处理完毕,那么至少要同时开动多少台机组?(每台机组每小时处理污水量不变)
小时内将污水处理完毕,那么至少要同时开动多少台机组?(每台机组每小时处理污水量不变)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小区为了绿化环境,计划分两次购进A、B两种花草,第一次分别购进A、B两种花草30棵和15棵,共花费675元;第二次分别购进A、B两种花草12棵和5棵![]() 两次共花费940元
两次共花费940元![]() 两次购进的A、B两种花草价格均分别相同
两次购进的A、B两种花草价格均分别相同![]() .
.
![]() 、B两种花草每棵的价格分别是多少元?
、B两种花草每棵的价格分别是多少元?
![]() 若再次购买A、B两种花草共12棵
若再次购买A、B两种花草共12棵![]() 、B两种花草价格不变
、B两种花草价格不变![]() ,且A种花草的数量不少于B种花草的数量的4倍,请你给出一种费用最省的方案,并求出该方案所需费用.
,且A种花草的数量不少于B种花草的数量的4倍,请你给出一种费用最省的方案,并求出该方案所需费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读对学生的成长有着深远的影响,某中学为了解学生每周课余阅读的时间,在本校随机抽取了若干名学生进行调查,并依据调查结果绘制了以下不完整的统计图表.
组别 | 时间 | 频数 | 频率 |
A |
| 6 |
|
B |
| a |
|
C |
| 10 |
|
D |
| 8 | b |
E |
| 4 |
|
合计 | 1 |
请根据图表中的信息,解答下列问题:
![]() 表中的
表中的![]() ______,
______,![]() ______,中位数落在______组,将频数分布直方图补全;
______,中位数落在______组,将频数分布直方图补全;
![]() 估计该校2000名学生中,每周课余阅读时间不足
估计该校2000名学生中,每周课余阅读时间不足![]() 小时的学生大约有多少名?
小时的学生大约有多少名?
![]() 组的4人中,有1名男生和3名女生,该校计划在E组学生中随机选出两人向全校同学作读书心得报告,请用画树状图或列表法求抽取的两名学生刚好是1名男生和1名女生的概率.
组的4人中,有1名男生和3名女生,该校计划在E组学生中随机选出两人向全校同学作读书心得报告,请用画树状图或列表法求抽取的两名学生刚好是1名男生和1名女生的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读对学生的成长有着深远的影响,某中学为了解学生每周课余阅读的时间,在本校随机抽取了若干名学生进行调查,并依据调查结果绘制了以下不完整的统计图表.
组别 | 时间(小时) | 频数(人数) | 频率 |
A | 0≤t≤0.5 | 6 | 0.15 |
B | 0.5≤t≤1 | a | 0.3 |
C | 1≤t≤1.5 | 10 | 0.25 |
D | 1.5≤t≤2 | 8 | b |
E | 2≤t≤2.5 | 4 | 0.1 |
合计 | 1 |
请根据图表中的信息,解答下列问题:
(1)表中的a= ,b= ,中位数落在 组,将频数分布直方图补全;
(2)估计该校2000名学生中,每周课余阅读时间不足0.5小时的学生大约有多少名?
(3)E组的4人中,有1名男生和3名女生,该校计划在E组学生中随机选出两人向全校同学作读书心得报告,请用画树状图或列表法求抽取的两名学生刚好是1名男生和1名女生的概率.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com