练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

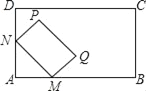
    【题目】如图，将矩形MNPQ放置在矩形ABCD中，使点M，N分别在AB，AD边上滑动，若MN=6，PN=4，在滑动过程中，点A与点P的距离AP的最大值为（　　）

    A. 4 B. 2 C. 7 D. 8

    【答案】D

    【解析】分析：如图所示，取MN中点E，当点A、E、P三点共线时，AP最大，利用勾股定理及直角三角形中斜边上的中线等于斜边的一半分别求出PE与AE的长，由AE+EP求出AP的最大值即可．

    详解：如图所示，取MN中点E，当点A、E、P三点共线时，AP最大，

    在Rt△PNE中，PN=4，NE=MN=3，
    根据勾股定理得：PE=，
    在Rt△AMN中，AE为斜边MN上的中线，
    ∴AE=MN=3，
    则AP的最大值为AE+EP=5+3=8．
    故选D．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】某超市计划在“十周年”庆典当天开展购物抽奖活动，凡当天在该超市购物的顾客，均有一次抽奖的机会，抽奖规则如下：将如图所示的圆形转盘平均分成四个扇形，分别标上1，2，3，4四个数字，抽奖者连续转动转盘两次，当每次转盘停止后指针所指扇形内的数为每次所得的数（若指针指在分界线时重转）；当两次所得数字之和为8时，返现金20元；当两次所得数字之和为7时，返现金15元；当两次所得数字之和为6时返现金10元．

    （1）试用树状图或列表的方法表示出一次抽奖所有可能出现的结果；

    （2）某顾客参加一次抽奖，能获得返还现金的概率是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某养殖户每年的养殖成本包括固定成本和可变成本，其中固定成本每年均为4万元，可变成本逐年增长，已知该养殖户第一年的可变成本为2.6万元，设可变成本平均每年增长的百分率为

    （1）用含x的代数式表示低3年的可变成本为 万元；

    （2）如果该养殖户第3年的养殖成本为7.146万元，求可变成本平均每年的增长百分率x.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，∠AOB＝30，∠AOB内有一定点P，且OP＝10．在OA上有一动点Q，OB上有一动点R．若ΔPQR周长最小，则最小周长是___________

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，△ABC的顶点坐标分别为A(1，3)、B(4，2)、C(2，1)．

    (1)作出与△ABC关于x轴对称的△A1B1C1，并写出A1、B1、C1的坐标；

    (2)以原点O为位似中心，在原点的另一侧画出△A2B2C2，使．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，四边形ABCD中，∠ABC＝90°，AB＝4，BC＝3，CD＝12，AD＝13．求四边形ABCD的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（1）如图1，AM∥CN，求证：

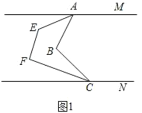
    ①∠MAB+∠ABC+∠BCN＝360°；

    ②∠MAE+∠AEF+∠EFC+∠FCN＝540°；

    （2）如图2，若平行线AM与CN间有n个点，根据（1）中的结论写出你的猜想并证明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】小烨在探究数轴上两点间距离时发现：若两点在轴上或与轴平行，两点的横坐标分别为，则两点间距离为；若两点在轴上或与轴平行，两点的纵坐标分别为，则两点间距离为.据此，小烨猜想：对于平面内任意两点，两点间的距离为.

    （1）请你利用下图，试证明：；

    （2）若，试在轴上求一点，使的距离最短，并求出的最小值和点坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

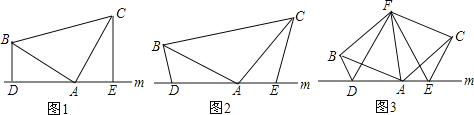
    【题目】(1)如图1，已知：在△ABC中，∠BAC=90°，AB=AC，直线m经过点A，BD⊥直线m，CE⊥直线m，垂足分别为点D、E．猜测DE、BD、CE三条线段之间的数量关系(直接写出结果即可)．

    (2)如图2，将(1)中的条件改为：在△ABC中，AB=AC，D、A、E三点都在直线m上，并且有∠BDA=∠AEC=∠BAC=α，其中α为任意锐角或钝角．请问第(1)题中DE、BD、CE之间的关系是否仍然成立？如成立，请你给出证明；若不成立，请说明理由．

    (3)拓展与应用：如图3，D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合)，点F为∠BAC平分线上的一点，且△ABF和△ACF均为等边三角形，连接BD、CE，若∠BDA=∠AEC=∠BAC，试判断线段DF、EF的数量关系，并说明理由．

    查看答案和解析>>

    同步练习册答案