
【题目】某超市计划在“十周年”庆典当天开展购物抽奖活动,凡当天在该超市购物的顾客,均有一次抽奖的机会,抽奖规则如下:将如图所示的圆形转盘平均分成四个扇形,分别标上1,2,3,4四个数字,抽奖者连续转动转盘两次,当每次转盘停止后指针所指扇形内的数为每次所得的数(若指针指在分界线时重转);当两次所得数字之和为8时,返现金20元;当两次所得数字之和为7时,返现金15元;当两次所得数字之和为6时返现金10元.
(1)试用树状图或列表的方法表示出一次抽奖所有可能出现的结果;
(2)某顾客参加一次抽奖,能获得返还现金的概率是多少?

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如果关于x的方程x2-ax+a2-3=0至少有一个正根,则实数a的取值范围是( )
A. -2<a<2 B. ![]() <a≤2 C.
<a≤2 C. ![]() <a≤2 D.
<a≤2 D. ![]() ≤a≤2
≤a≤2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:有一个内角为90°,且对角线相等的四边形称为准矩形.

(1)①如图1,准矩形ABCD中,∠ABC=90°,若AB=2,BC=3,则BD= ;
②如图2,直角坐标系中,A(0,3),B(5,0),若整点P使得四边形AOBP是准矩形,则点P的坐标是 ;(整点指横坐标、纵坐标都为整数的点)
(2)如图3,正方形ABCD中,点E、F分别是边AD、AB上的点,且CF⊥BE,求证:四边形BCEF是准矩形;
(3)已知,准矩形ABCD中,∠ABC=90°,∠BAC=60°,AB=2,当△ADC为等腰三角形时,请直接写出这个准矩形的面积是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A,B,C三点在同一直线上,分别以AB,BC(AB>BC)为边,在直线AC的同侧作等边ΔABD和等边ΔBCE,连接AE交BD于点M,连接CD交BE于点N,连接MN. 以下结论:①AE=DC,②MN//AB,③BD⊥AE,④∠DPM=60°,⑤ΔBMN是等边三角形.其中正确的是__________(把所有正确的序号都填上).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】推理填空:
如图,已知∠1=∠2,∠B=∠C,可推得AB∥CD.理由如下:
∵∠1=∠2(已知),且∠1=∠4( )
∴∠2=∠4 (等量代换)
∴CE∥BF ( )
∴∠ =∠3( )
又∵∠B=∠C(已知),∴∠3=∠B(等量代换)
∴AB∥CD ( )

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图△ABC三个顶点的坐标分别为A(0,﹣3)、B(3,﹣2)、C(2,﹣4),正方形网格中,每个小正方形的边长是1个单位长度.
(1)画出△ABC向上平移6个单位得到的△A1B1C1;
(2)以点C为位似中心,在网格中画出△A2B2C2,使△A2B2C2与△ABC位似,且△A2B2C2与△ABC的位似比为2:1,并直接写出点A2的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)定义:直角三角形两直角边的平方和等于斜边的平方。如:直角三角形的直角边分别为3、4,则斜边的平方=32+42=25.已知:Rt△ABC中,∠C=90°,AC=8,AB=10,直接写出BC2=___.

(2)应用:已知正方形ABCD的边长为4,点P为AD边上的一点,AP=![]() AD,请利用“两点之间线段最短”这一原理,在线段AC上画出一点M,使MP+MD最小,并直接写出最小值的平方为多少?
AD,请利用“两点之间线段最短”这一原理,在线段AC上画出一点M,使MP+MD最小,并直接写出最小值的平方为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABE中,∠BAE=105°,AE的垂直平分线MN交BE于点C,且AB=CE,则∠B的度数是( )

A. 45°B. 60°C. 50°D. 55°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形MNPQ放置在矩形ABCD中,使点M,N分别在AB,AD边上滑动,若MN=6,PN=4,在滑动过程中,点A与点P的距离AP的最大值为( )
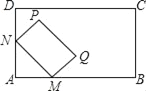
A. 4 B. 2![]() C. 7 D. 8
C. 7 D. 8
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com