
【题目】定义:有一个内角为90°,且对角线相等的四边形称为准矩形.

(1)①如图1,准矩形ABCD中,∠ABC=90°,若AB=2,BC=3,则BD= ;
②如图2,直角坐标系中,A(0,3),B(5,0),若整点P使得四边形AOBP是准矩形,则点P的坐标是 ;(整点指横坐标、纵坐标都为整数的点)
(2)如图3,正方形ABCD中,点E、F分别是边AD、AB上的点,且CF⊥BE,求证:四边形BCEF是准矩形;
(3)已知,准矩形ABCD中,∠ABC=90°,∠BAC=60°,AB=2,当△ADC为等腰三角形时,请直接写出这个准矩形的面积是 .
【答案】(1)![]() (2)(5,3),(3,5)(3)
(2)(5,3),(3,5)(3)![]() ;
;![]() ;
;![]()
【解析】试题分析:(1)利用准矩形的定义和勾股定理计算,再根据准矩形的特点和整点的特点求出即可;
(2)先利用正方形的性质判断出△ABE≌△BCF,即可;
(2)分三种情况分别计算,用到梯形面积公式,对角线面积公式,对角线互相垂直的四边形的面积计算方法.
试题解析:(1)①∵∠ABC=90,
∴BD=![]() ,
,
故答案为![]() ,
,
②∵A(0,3),B(5,0),
∴AB=![]() =6,
=6,
设点P(m,n),A(0,0),
∴OP=![]() =6,
=6,
∵m,n都为整数,
∴点P(3,5)或(5,3);
故答案为P(3,5)或(5,3);
(2)∵四边形ABCD是正方形,
∴AB=BC∠A=∠ABC=90°,
∴∠EAF+∠EBC=90°,
∵BE⊥CF,
∴∠EBC+∠BCF=90°,
∴∠EBF=∠BCF,
∴△ABE≌△BCF,
∴BE=CF,
∴四边形BCEF是准矩形;
(3)![]() ;
;![]() ;
;![]()
∵∠ABC=90°,∠BAC=60°,AB=2,
∴BC=2![]() ,AC=4,
,AC=4,
准矩形ABCD中,BD=AC=4,
①当AC=AD时,如图1,作DE⊥AB,
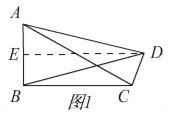
∴AE=BE![]() AB=1,
AB=1,
∴DE=![]() ,
,
∴S准矩形ABCD=S△ADE+S梯形BCDE
=![]() DE×AE+
DE×AE+![]() (BC+DE)×BE
(BC+DE)×BE
=![]() ×
×![]() +
+![]() (2
(2![]() +
+![]() )×1
)×1
=![]() +
+![]() ;
;
②当AC=CD时,如图2,
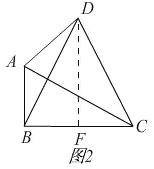
作DF⊥BC,
∴BD=CD,
∴BF=CF=![]() BC=
BC=![]() ,
,
∴DF=![]() ,
,
∴S准矩形ABCD=S△DCF+S梯形ABFD
=![]() FC×DF+
FC×DF+![]() (AB+DF)×BF
(AB+DF)×BF
=![]() ×
×![]() ×
×![]() +
+![]() (2+
(2+![]() )×
)×![]()
=![]() +
+![]() ;
;
③当AD=CD,如图3,

连接AC中点和D并延长,连接BG,过B作BH⊥DG,
∴BD=CD=AC=4,
∴AG=![]() AC=2,
AC=2,
∵AB=2,
∴AB=AG,
∵∠BAC=60°,
∴∠ABG=60°,
∴∠CBG=30°
在Rt△BHG中,BG=2,∠BGH=30°,
∴BH=1,
在Rt△BHM中,BH=1,∠CBH=30°,
∴BM=![]() ,HM=
,HM=![]() ,
,
∴CM=![]() ,
,
在Rt△DHB中,BH=1,BD=4,
∴DH=![]() ,∴DM=DH﹣MH=
,∴DM=DH﹣MH=![]() ﹣
﹣![]() ,
,
∴S准矩形ABCD=S△DCF+S四边形AMCD
=![]() BM×AB+
BM×AB+![]() AC×DM
AC×DM
=![]() ×
×![]() ×2+
×2+![]() ×4×(
×4×(![]() ﹣
﹣![]() )
)
=2![]() ;
;
故答案为![]() ;
;![]() ;
;![]() .
.


 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案科目:初中数学 来源: 题型:
【题目】黔东南州某校吴老师组织九(1)班同学开展数学活动,带领同学们测量学校附近一电线杆的高.已知电线杆直立于地面上,某天在太阳光的照射下,电线杆的影子(折线BCD)恰好落在水平地面和斜坡上,在D处测得电线杆顶端A的仰角为30°,在C处测得电线杆顶端A得仰角为45°,斜坡与地面成60°角,CD=4m,请你根据这些数据求电线杆的高AB.
(结果精确到1m,参考数据:![]() ≈1.4,
≈1.4,![]() ≈1.7)
≈1.7)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BP平分∠ABC,D为BP上一点,E,F分别在BA,BC上,且满足DE=DF,若∠BED=140°,则∠BFD的度数是( )

A. 40°B. 50°C. 60°D. 70°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市为了回馈广大新老客户,元旦期间决定实行优惠活动.方案一:非会员购物所有商品价格可获九折优惠;方案二:交纳![]() 元会费成为该超市的会员,所有商品价格可获八折优惠.
元会费成为该超市的会员,所有商品价格可获八折优惠.
(1)若用![]() (元)表示商品价格,请你用含
(元)表示商品价格,请你用含![]() 的式子分别表示两种购物方案所付的钱数.
的式子分别表示两种购物方案所付的钱数.
(2)当商品价格是多少元时,两种方案所付钱数相同?
(3)若你计划在该超市购买商品,请分析选择哪种方案更省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有理数的计算:
(1)1﹣(﹣8)+12+(﹣11);
(2)|﹣![]() |
|![]() ;
;
(3)﹣12﹣(1﹣![]() )
)![]() ×[6+(﹣3)3];
×[6+(﹣3)3];
(4)![]() ×(﹣6)2﹣5.5×8+25.5×8.
×(﹣6)2﹣5.5×8+25.5×8.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面关于x的方程中:①ax2+x+2=0;②3(x-9)2-(x+1)2=1;③x+3=![]() ④x2-a=0(a为任意实数
④x2-a=0(a为任意实数![]() ;⑤
;⑤![]() =x-1一元二次方程的个数是
=x-1一元二次方程的个数是![]()
![]()
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个口袋中放有290个涂有红、黑、白三种颜色的质地相同的小球.若红球个数是黑球个数的2倍多40个.从袋中任取一个球是白球的概率是![]() .
.
(1)求袋中红球的个数;
(2)求从袋中任取一个球是黑球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市计划在“十周年”庆典当天开展购物抽奖活动,凡当天在该超市购物的顾客,均有一次抽奖的机会,抽奖规则如下:将如图所示的圆形转盘平均分成四个扇形,分别标上1,2,3,4四个数字,抽奖者连续转动转盘两次,当每次转盘停止后指针所指扇形内的数为每次所得的数(若指针指在分界线时重转);当两次所得数字之和为8时,返现金20元;当两次所得数字之和为7时,返现金15元;当两次所得数字之和为6时返现金10元.
(1)试用树状图或列表的方法表示出一次抽奖所有可能出现的结果;
(2)某顾客参加一次抽奖,能获得返还现金的概率是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某养殖户每年的养殖成本包括固定成本和可变成本,其中固定成本每年均为4万元,可变成本逐年增长,已知该养殖户第一年的可变成本为2.6万元,设可变成本平均每年增长的百分率为![]()
(1)用含x的代数式表示低3年的可变成本为 万元;
(2)如果该养殖户第3年的养殖成本为7.146万元,求可变成本平均每年的增长百分率x.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com