
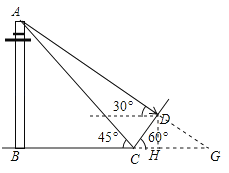
【题目】黔东南州某校吴老师组织九(1)班同学开展数学活动,带领同学们测量学校附近一电线杆的高.已知电线杆直立于地面上,某天在太阳光的照射下,电线杆的影子(折线BCD)恰好落在水平地面和斜坡上,在D处测得电线杆顶端A的仰角为30°,在C处测得电线杆顶端A得仰角为45°,斜坡与地面成60°角,CD=4m,请你根据这些数据求电线杆的高AB.
(结果精确到1m,参考数据:![]() ≈1.4,
≈1.4,![]() ≈1.7)
≈1.7)

【答案】11m.
【解析】
试题分析:延长AD交BC的延长线于G,作DH⊥BG于H,由三角函数求出求出CH、DH的长,得出CG,设AB=xm,根据正切的定义求出BG,得出方程,解方程即可.
试题解析:延长AD交BC的延长线于G,作DH⊥BG于H,如图所示:
在Rt△DHC中,∠DCH=60°,CD=4,则CH=CDcos∠DCH=4×cos60°=2,DH=CDsin∠DCH=4×sin60°=![]() ,∵DH⊥BG,∠G=30°,∴HG=
,∵DH⊥BG,∠G=30°,∴HG=![]() =
=![]() =6,∴CG=CH+HG=2+6=8,设AB=xm,∵AB⊥BG,∠G=30°,∠BCA=45°,∴BC=x,BG=
=6,∴CG=CH+HG=2+6=8,设AB=xm,∵AB⊥BG,∠G=30°,∠BCA=45°,∴BC=x,BG=![]() =
=![]() =
=![]() x,∵BG﹣BC=CG,∴
x,∵BG﹣BC=CG,∴![]() x﹣x=8,解得:x≈11(m);
x﹣x=8,解得:x≈11(m);
答:电线杆的高为11m.


科目:初中数学 来源: 题型:
【题目】在如图所示的平面直角坐标系中,
(1)画出函数![]() 的图象;
的图象;
(2)填空:请写出图象与x轴的交点A(___,___)的坐标,与y轴交点B(___,__)的坐标;
(3)在(2)的条件下,求出△AOB的面积;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于点D,DE⊥AB,垂足为E,且AB=6cm,则△DEB的周长为( )

A. 4cm B. 6cm C. 8cm D. 10cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角三角形ABC中,∠ABC=90°.

(1)先作∠ACB的平分线;设它交AB边于点O,再以点O为圆心,OB为半径作⊙O(尺规作图,保留作图痕迹,不写作法);
(2)证明:AC是所作⊙O的切线;
(3)若BC=![]() ,∠A=30°,求△AOC的面积.
,∠A=30°,求△AOC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某校教学楼AB后方有一斜坡,已知斜坡CD的长为12米,坡角α为60°,根据有关部门的规定,∠α≤39°时,才能避免滑坡危险,学校为了消除安全隐患,决定对斜坡CD进行改造,在保持坡脚C不动的情况下,学校至少要把坡顶D向后水平移动多少米才能保证教学楼的安全?(结果取整数)
(参考数据:sin39°≈0.63,cos39°≈0.78,tan39°≈0.81,![]() ≈1.41,
≈1.41,![]() ≈1.73,
≈1.73,![]() ≈2.24)
≈2.24)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车分别从A,B两地同时相向匀速行驶,当乙车到达A地后,继续保持原速向远离B的方向行驶,而甲车到达B地后立即掉头,并保持原速与乙车同向行驶,经过15小时后两车同时到达距A地300千米的C地(中途休息时间忽略不计).设两车行驶的时间为x(小时),两车之间的距离为y(千米),y与x之间的函数关系如图所示,则当甲车到达B地时,乙车距A地_____千米.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC为⊙O的直径,AC=4,B、D分别在AC两侧的圆上,∠BAD=60°,BD与AC的交点为E.

(1)求点O到BD的距离及∠OBD的度数;
(2)若DE=2BE,求![]() 的值和CD的长.
的值和CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果关于x的方程x2-ax+a2-3=0至少有一个正根,则实数a的取值范围是( )
A. -2<a<2 B. ![]() <a≤2 C.
<a≤2 C. ![]() <a≤2 D.
<a≤2 D. ![]() ≤a≤2
≤a≤2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:有一个内角为90°,且对角线相等的四边形称为准矩形.

(1)①如图1,准矩形ABCD中,∠ABC=90°,若AB=2,BC=3,则BD= ;
②如图2,直角坐标系中,A(0,3),B(5,0),若整点P使得四边形AOBP是准矩形,则点P的坐标是 ;(整点指横坐标、纵坐标都为整数的点)
(2)如图3,正方形ABCD中,点E、F分别是边AD、AB上的点,且CF⊥BE,求证:四边形BCEF是准矩形;
(3)已知,准矩形ABCD中,∠ABC=90°,∠BAC=60°,AB=2,当△ADC为等腰三角形时,请直接写出这个准矩形的面积是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com