练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】下面关于x的方程中：①ax2+x+2=0；②3（x-9）2-（x+1）2=1；③x+3=④x2-a=0（a为任意实数；⑤=x-1一元二次方程的个数是　　

    A. 1 B. 2 C. 3 D. 4

    【答案】B

    【解析】

    根据一元二次方程的定义:只含有一个未知数,并且未知数的最高指数是2的整式方程, 且二次项系数不等于0,即可进行判定,

    ①ax2+x+2=0, 中二次项系数有可能为0, 不一定是一元二次方程, 不符合题意,

    ②3(x-9)2-(x+1)2=1符合一元二次方程的定义,符合题意,③因为未知数出现在分母上,是分式方程,不符合题意,④x2-a=0（a为任意实数）,符合一元二次方程的定义,符合题意,⑤是无理方程,不符合题意,因此属于一元二次方程的共有2个,

    故选B.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】甲、乙两车分别从A，B两地同时相向匀速行驶，当乙车到达A地后，继续保持原速向远离B的方向行驶，而甲车到达B地后立即掉头，并保持原速与乙车同向行驶，经过15小时后两车同时到达距A地300千米的C地（中途休息时间忽略不计）．设两车行驶的时间为x（小时），两车之间的距离为y（千米），y与x之间的函数关系如图所示，则当甲车到达B地时，乙车距A地_____千米．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，边AB、AC的垂直平分线分别交BC于D、E．

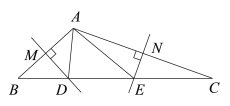
    （1）若BC=5，求△ADE的周长．

    （2）若∠BAD+∠CAE=60°，求∠BAC的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知△ABC中，D是BC边上的一点，E是AD的中点，过A点作BC的平行线，交CE的延长线于点F，且AF=BD，连接BF．

    （1）求证：BD=CD；（2）如果AB=AC，试判断四边形AFBD的形状，并证明你的结论．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】定义：有一个内角为90°，且对角线相等的四边形称为准矩形．

    （1）①如图1，准矩形ABCD中，∠ABC=90°，若AB=2，BC=3，则BD=　 　；

    ②如图2，直角坐标系中，A（0，3），B（5，0），若整点P使得四边形AOBP是准矩形，则点P的坐标是　 　；（整点指横坐标、纵坐标都为整数的点）

    （2）如图3，正方形ABCD中，点E、F分别是边AD、AB上的点，且CF⊥BE，求证：四边形BCEF是准矩形；

    （3）已知，准矩形ABCD中，∠ABC=90°，∠BAC=60°，AB=2，当△ADC为等腰三角形时，请直接写出这个准矩形的面积是　 　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图①，△ABC中，AB=AC，∠B、∠C的平分线交于O点，过O点作EF∥BC交AB、AC于E、F．试回答：

    （1）图中等腰三角形是 ．猜想：EF与BE、CF之间的关系是 ．理由：

    （2）如图②，若AB≠AC，图中等腰三角形是 ．在第（1）问中EF与BE、CF间的关系还存在吗？

    （3）如图③，若△ABC中∠B的平分线BO与三角形外角平分线CO交于O，过O点作OE∥BC交AB于E，交AC于F．这时图中还有等腰三角形吗？EF与BE、CF关系又如何？说明你的理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图,A,B,C三点在同一直线上,分别以AB,BC（AB>BC）为边,在直线AC的同侧作等边ΔABD和等边ΔBCE,连接AE交BD于点M,连接CD交BE于点N,连接MN. 以下结论：①AE=DC，②MN//AB，③BD⊥AE，④∠DPM=60°，⑤ΔBMN是等边三角形.其中正确的是__________（把所有正确的序号都填上）.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：如图△ABC三个顶点的坐标分别为A（0，﹣3）、B（3，﹣2）、C（2，﹣4），正方形网格中，每个小正方形的边长是1个单位长度．

    （1）画出△ABC向上平移6个单位得到的△A1B1C1；

    （2）以点C为位似中心，在网格中画出△A2B2C2，使△A2B2C2与△ABC位似，且△A2B2C2与△ABC的位似比为2：1，并直接写出点A2的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在正方形ABCD中．


    （1）若点E、F分别在AB、AD上，且AE=DF．试判断DE与CF的数量及位置关系，并说明理由；
    （2）若P、Q、M、N是正方形ABCD各边上的点，PQ与MN相交，且PQ=MN，问PQ⊥MN成立吗？为什么？

    查看答案和解析>>

    同步练习册答案