
【题目】如图,在正方形ABCD中.

(1)若点E、F分别在AB、AD上,且AE=DF.试判断DE与CF的数量及位置关系,并说明理由;
(2)若P、Q、M、N是正方形ABCD各边上的点,PQ与MN相交,且PQ=MN,问PQ⊥MN成立吗?为什么?
【答案】(1)DE=CF,DE⊥CF.理由见解析;(2)MN⊥PQ成立,理由见解析;
【解析】
(1)由已知易得△DAE≌△CDF,故有DE=CF.
(2)由点N,Q分别向AB,AD作垂线,构造两直角三角形全等,由角的等量代换,易得QP⊥MN.
(1)在正方形ABCD中,AD=DC,AE=DF,∠EAD=∠FDC,
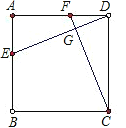
所以△EAD≌△FDC,故DE=CF,
∴∠EDA=∠FCD,
又∵∠DCF+∠DFC=90°,
∴∠ADE+∠DFC=90°,
∴∠DGF=90°
即DE⊥CF.
(2)由点N,Q分别向AB,AD作垂线,
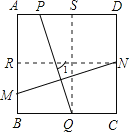
∵PQ=MN,RN=SQ,
∴△MNR≌△QPS(HL),
∴∠PQS=∠MNR,又∠1+∠PQS=90°,
所以∠1+∠MNR=90°,即MN⊥PQ.


科目:初中数学 来源: 题型:
【题目】下面关于x的方程中:①ax2+x+2=0;②3(x-9)2-(x+1)2=1;③x+3=![]() ④x2-a=0(a为任意实数
④x2-a=0(a为任意实数![]() ;⑤
;⑤![]() =x-1一元二次方程的个数是
=x-1一元二次方程的个数是![]()
![]()
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】菱形AOBC如图放置,A(3,4),先将菱形向左平移9个单位长度,再向下平移1个单位,然后沿x轴翻折,最后绕坐标轴原点O旋转90°得到点C的对应点为点P,则点P的坐标为______.
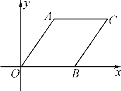
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在矩形ABCD中,M、N分别是边AD、BC的中点,E、F分别是线段BM、CM的中点
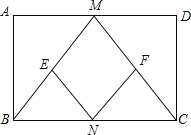
(1)求证:△ABM≌△DCM
(2)判断四边形MENF是什么特殊四边形,并证明你的结论;
(3)当AD:AB= _时,四边形MENF是正方形(只写结论,不需证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某养殖户每年的养殖成本包括固定成本和可变成本,其中固定成本每年均为4万元,可变成本逐年增长,已知该养殖户第一年的可变成本为2.6万元,设可变成本平均每年增长的百分率为![]()
(1)用含x的代数式表示低3年的可变成本为 万元;
(2)如果该养殖户第3年的养殖成本为7.146万元,求可变成本平均每年的增长百分率x.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系xOy中,点A、B的横坐标分别为a、![]() ,二次函数
,二次函数![]() 的图象经过点A、B,且a、m满足
的图象经过点A、B,且a、m满足![]() 为常数
为常数![]() .
.
![]() 若一次函数
若一次函数![]() 的图象经过A、B两点.
的图象经过A、B两点.
![]() 当
当![]() 、
、![]() 时,求k的值;
时,求k的值;
![]() 若y随x的增大而减小,求d的取值范围;
若y随x的增大而减小,求d的取值范围;
![]() 当
当![]() 且
且![]() 、
、![]() 时,判断直线AB与x轴的位置关系,并说明理由;
时,判断直线AB与x轴的位置关系,并说明理由;
![]() 点A、B的位置随着a的变化而变化,设点A、B运动的路线与y轴分别相交于点C、D,线段CD的长度会发生变化吗?如果不变,求出CD的长;如果变化,请说明理由.
点A、B的位置随着a的变化而变化,设点A、B运动的路线与y轴分别相交于点C、D,线段CD的长度会发生变化吗?如果不变,求出CD的长;如果变化,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB=30,∠AOB内有一定点P,且OP=10.在OA上有一动点Q,OB上有一动点R.若ΔPQR周长最小,则最小周长是___________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工程队用甲、乙两台隧道挖掘机从两个方向挖掘同一条隧道,因为地质条件不同,甲、乙的挖掘速度不同,已知甲、乙同时挖掘![]() 天,可以挖
天,可以挖![]() 米,若甲挖
米,若甲挖![]() 天,乙挖
天,乙挖![]() 天可以挖掘
天可以挖掘![]() 米.
米.
(1)请问甲、乙挖掘机每天可以挖掘多少米?
(2)若乙挖掘机比甲挖掘每小时多挖掘![]() 米,甲、乙每天挖掘的时间相同,求甲每小时挖掘多少米?
米,甲、乙每天挖掘的时间相同,求甲每小时挖掘多少米?
(3)若隧道的总长为![]() 米,甲、乙挖掘机工作
米,甲、乙挖掘机工作![]() 天后,因为甲挖掘机进行设备更新,乙挖掘机设备老化,甲比原来每天多挖
天后,因为甲挖掘机进行设备更新,乙挖掘机设备老化,甲比原来每天多挖![]() 米,同时乙比原来少挖
米,同时乙比原来少挖![]() 米
米![]() .最终,甲、乙两台挖掘机在相同时间里各完成隧道总长的一半,请用含
.最终,甲、乙两台挖掘机在相同时间里各完成隧道总长的一半,请用含![]() ,
,![]() 的代数式表示
的代数式表示![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com