
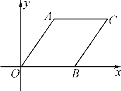
【题目】菱形AOBC如图放置,A(3,4),先将菱形向左平移9个单位长度,再向下平移1个单位,然后沿x轴翻折,最后绕坐标轴原点O旋转90°得到点C的对应点为点P,则点P的坐标为______.
【答案】(-3,1)或(3,-1)
【解析】
根据菱形的对称性求出点B的坐标,再求出AB的中点的坐标,进而求出点C的坐标,根据向左平移横坐标减,向下平移纵坐标减求出平移后的C点对应的坐标,结合翻折变换知识求出沿x轴翻折后C点对应的坐标,再根据旋转的性质确定点P的坐标.
∵菱形AOBC的点A坐标为(3,4),
∴点B的坐标为(5,0),
∴AB的中点的坐标为(4,2),
∴点C坐标为(8,4),
∵向左平移9个单位长度,再向下平移1个单位长度,
∴8-9=-1,4-1=3,
∴平移后点C对应的坐标为(-1,3),
沿x轴翻折后C点对应的坐标为(-1,-3),
∵在坐标平面内绕点O旋转90°,
∴若是顺时针旋转,则对应点在第二象限,坐标为(-3,1),
若是逆时针旋转,则对应点在第四象限,坐标为(3,-1),
综上所述,点P的坐标为(-3,1)或(3,-1),
故答案为:(-3,1)或(3,-1),


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,边AB、AC的垂直平分线分别交BC于D、E.
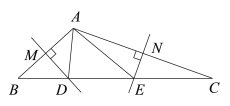
(1)若BC=5,求△ADE的周长.
(2)若∠BAD+∠CAE=60°,求∠BAC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A,B,C三点在同一直线上,分别以AB,BC(AB>BC)为边,在直线AC的同侧作等边ΔABD和等边ΔBCE,连接AE交BD于点M,连接CD交BE于点N,连接MN. 以下结论:①AE=DC,②MN//AB,③BD⊥AE,④∠DPM=60°,⑤ΔBMN是等边三角形.其中正确的是__________(把所有正确的序号都填上).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图△ABC三个顶点的坐标分别为A(0,﹣3)、B(3,﹣2)、C(2,﹣4),正方形网格中,每个小正方形的边长是1个单位长度.
(1)画出△ABC向上平移6个单位得到的△A1B1C1;
(2)以点C为位似中心,在网格中画出△A2B2C2,使△A2B2C2与△ABC位似,且△A2B2C2与△ABC的位似比为2:1,并直接写出点A2的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)定义:直角三角形两直角边的平方和等于斜边的平方。如:直角三角形的直角边分别为3、4,则斜边的平方=32+42=25.已知:Rt△ABC中,∠C=90°,AC=8,AB=10,直接写出BC2=___.

(2)应用:已知正方形ABCD的边长为4,点P为AD边上的一点,AP=![]() AD,请利用“两点之间线段最短”这一原理,在线段AC上画出一点M,使MP+MD最小,并直接写出最小值的平方为多少?
AD,请利用“两点之间线段最短”这一原理,在线段AC上画出一点M,使MP+MD最小,并直接写出最小值的平方为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
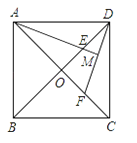
【题目】(8分)如图,在正方形ABCD中,对角线AC、BD相交于O,E、F分别在OD、OC上,且DE=CF,连结DF、AE,AE的延长线交于DF于点M,求证:AM⊥DF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABE中,∠BAE=105°,AE的垂直平分线MN交BE于点C,且AB=CE,则∠B的度数是( )

A. 45°B. 60°C. 50°D. 55°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中.

(1)若点E、F分别在AB、AD上,且AE=DF.试判断DE与CF的数量及位置关系,并说明理由;
(2)若P、Q、M、N是正方形ABCD各边上的点,PQ与MN相交,且PQ=MN,问PQ⊥MN成立吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在我市中小学标准化建设工程中,某学校计划购进一批电脑和电子白板,经过市场考察得知,购买1台电脑和2台电子白板需要3.5万元,购买2台电脑和1台电子白板需要2.5万元.
(1)求每台电脑、每台电子白板各多少万元?
(2)根据学校实际,需购进电脑和电子白板共30台,总费用不超过30万元,但不低于28万元,该校有几种购买方案?
(3)上面的哪种方案费用最低?按费用最低方案购买需要多少钱?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com