
【题目】如图,A,B,C三点在同一直线上,分别以AB,BC(AB>BC)为边,在直线AC的同侧作等边ΔABD和等边ΔBCE,连接AE交BD于点M,连接CD交BE于点N,连接MN. 以下结论:①AE=DC,②MN//AB,③BD⊥AE,④∠DPM=60°,⑤ΔBMN是等边三角形.其中正确的是__________(把所有正确的序号都填上).

【答案】①②④⑤
【解析】
①由三角形ABD与三角形BCE都为等边三角形,利用等边三角形的性质得到两条边对应相等,两个角相等都为60°,利用SAS即可得到三角形ABE与三角形DBC全等即可得结论;
②由①中三角形ABE与三角形DBC全等,利用全等三角形的对应角相等得到一对角相等,再由∠ABD=∠EBC=60°,利用平角的定义得到∠MBE=∠NBC=60°,再由EB=CB,利用ASA可得出三角形EMB与三角形CNB全等,利用全等三角形的对应边相等得到MB=NB,再由∠MBE=60°,利用有一个角为60°的等腰三角形为等边三角形可得出三角形BMN为等边三角形;可得∠BMN=60°,进行可得∠BMN=∠ABD,故MN//AB,从而可判断②,⑤正确;
③无法证明PM=PN,因此不能得到BD⊥AE;
④由①得∠EAB=∠CDB,根据三角形内角和和外角的性质可证得结论.
①∵等边△ABD和等边△BCE,
∴AB=DB,BE=BC,∠ABD=∠EBC=60°,
∴∠ABE=∠DBC=120°,
在△ABE和△DBC中,
∵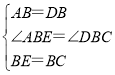 ,
,
∴△ABE≌△DBC(SAS),
∴AE=DC,
故①正确;
∵△ABE≌△DBC,
∴∠AEB=∠DCB,
又∠ABD=∠EBC=60°,
∴∠MBE=180°-60°-60°=60°,
即∠MBE=∠NBC=60°,
在△MBE和△NBC中,
∵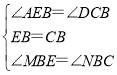 ,
,
∴△MBE≌△NBC(ASA),
∴BM=BN,∠MBE=60°,
则△BMN为等边三角形,
故⑤正确;
∵△BMN为等边三角形,
∴∠BMN=60°,
∵∠ABD=60°,
∴∠BMN=∠ABD,
∴MN//AB,
故②正确;
③无法证明PM=PN,因此不能得到BD⊥AE;
④由①得∠EAB=∠CDB,∠APC+∠PAC+∠PCA=180°,
∴∠PAC+∠PCA=∠PDB+∠PCB=∠DBA=60°,
∵∠DPM =∠PAC+∠PCA
∴∠DPM =60°,故④正确,
故答案为:①②④⑤.


科目:初中数学 来源: 题型:
【题目】小亮家距离学校8千米,昨天早晨,小亮骑车上学途中,自行车“爆胎”,恰好路边有“自行车”维修部,几分钟后车修好了,为了不迟到,他加快了骑车到校的速度.回校后,小亮根据这段经历画出如下图象.该图象描绘了小亮行的路程S与他所用的时间t之间的关系.请根据图象,解答下列问题:
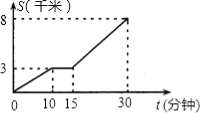
(1)小亮行了多少千米时,自行车“爆胎”?修车用了几分钟?
(2)小亮到校路上共用了多少时间?
(3)如果自行车没有“爆胎”,一直用修车前的速度行驶,那么他比实际情况早到或晚到学校多少分钟(精确到0.1)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市为了回馈广大新老客户,元旦期间决定实行优惠活动.方案一:非会员购物所有商品价格可获九折优惠;方案二:交纳![]() 元会费成为该超市的会员,所有商品价格可获八折优惠.
元会费成为该超市的会员,所有商品价格可获八折优惠.
(1)若用![]() (元)表示商品价格,请你用含
(元)表示商品价格,请你用含![]() 的式子分别表示两种购物方案所付的钱数.
的式子分别表示两种购物方案所付的钱数.
(2)当商品价格是多少元时,两种方案所付钱数相同?
(3)若你计划在该超市购买商品,请分析选择哪种方案更省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面关于x的方程中:①ax2+x+2=0;②3(x-9)2-(x+1)2=1;③x+3=![]() ④x2-a=0(a为任意实数
④x2-a=0(a为任意实数![]() ;⑤
;⑤![]() =x-1一元二次方程的个数是
=x-1一元二次方程的个数是![]()
![]()
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个口袋中放有290个涂有红、黑、白三种颜色的质地相同的小球.若红球个数是黑球个数的2倍多40个.从袋中任取一个球是白球的概率是![]() .
.
(1)求袋中红球的个数;
(2)求从袋中任取一个球是黑球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读下列材料,再解答下列问题:
题:分解因式:![]()
解:将“![]() ”看成整体,设
”看成整体,设![]() ,则原式=
,则原式=![]()
![]()
再将“![]() ”还原,得原式=
”还原,得原式=![]() .
.
上述解题用到的是“整体思想”,“整体思想”是数学解题中常用的一种思想方法,请你仿照上面的方法解答下列问题:
(1)因式分解:![]() ;
;![]() .
.
(2)因式分解:![]() ;
;![]() .
.
(3)求证:若![]() 为正整数,则式子
为正整数,则式子![]() 的值一定是某一个正整数的平方.
的值一定是某一个正整数的平方.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市计划在“十周年”庆典当天开展购物抽奖活动,凡当天在该超市购物的顾客,均有一次抽奖的机会,抽奖规则如下:将如图所示的圆形转盘平均分成四个扇形,分别标上1,2,3,4四个数字,抽奖者连续转动转盘两次,当每次转盘停止后指针所指扇形内的数为每次所得的数(若指针指在分界线时重转);当两次所得数字之和为8时,返现金20元;当两次所得数字之和为7时,返现金15元;当两次所得数字之和为6时返现金10元.
(1)试用树状图或列表的方法表示出一次抽奖所有可能出现的结果;
(2)某顾客参加一次抽奖,能获得返还现金的概率是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
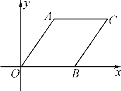
【题目】菱形AOBC如图放置,A(3,4),先将菱形向左平移9个单位长度,再向下平移1个单位,然后沿x轴翻折,最后绕坐标轴原点O旋转90°得到点C的对应点为点P,则点P的坐标为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB=30,∠AOB内有一定点P,且OP=10.在OA上有一动点Q,OB上有一动点R.若ΔPQR周长最小,则最小周长是___________

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com