
����Ŀ��С���Ҿ���ѧУ8ǧ���������糿��С���ﳵ��ѧ;�У����г�����̥����ǡ��·���С����г���ά���������Ӻ����ˣ�Ϊ�˲��ٵ������ӿ����ﳵ��У���ٶȣ���У��С��������ξ�����������ͼ��ͼ�������С���е�·��S�������õ�ʱ��t֮��Ĺ�ϵ�������ͼ����������⣺
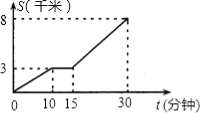
��1��С�����˶���ǧ��ʱ�����г�����̥���������˼����ӣ�
��2��С����У·�Ϲ����˶���ʱ�䣿
��3��������г�û�С���̥����һֱ����ǰ���ٶ���ʻ����ô����ʵ������絽������ѧУ���ٷ��ӣ���ȷ��0.1����
���𰸡���1��3ǧ����������15��10=5�����ӣ�����2��30���ӣ���3������ʵ������絽ѧУ3.3���ӣ�
��������
������һ������ͼ��,��Ҫ�����x���y���ʾʲô,ˮƽ�߱�ʾyû�仯,����ֱ�߱�ʾy��������,ֱ�ߵ�б�ʾ������ӵ��ٶ�,��1������,��10����ʱ,Sû�仯,˵���ڴ˴���̥,С������3ǧ��ʱ�����г�����̥���������ʱ��һֱ��15����,��������15��10=5�����ӣ�����2����ͼ����ֱ�ӿ��Կ���С����У·�Ϲ�����30���ӣ���3��С����ǰ���ٶ�Ϊ3��10=![]() ��ǧ��/���ӣ��������ٶȵ�У����ʱ��Ϊ8��
��ǧ��/���ӣ��������ٶȵ�У����ʱ��Ϊ8��![]() =
=![]() �����ӣ���30-
�����ӣ���30-![]() =
=![]() ��3.3�����ӣ���������ʵ������絽ѧУ3.3���ӣ�
��3.3�����ӣ���������ʵ������絽ѧУ3.3���ӣ�
�����������1������,��10����ʱ,Sû�仯,˵���ڴ˴���̥,С������3ǧ��ʱ�����г�����̥����
�����ʱ��һֱ��15����,��������15��10=5�����ӣ���
��2����ͼ����ֱ�ӿ��Կ���С����У·�Ϲ�����30���ӣ�
��3��С����ǰ���ٶ�Ϊ3��10=![]() ��ǧ��/���ӣ���
��ǧ��/���ӣ���
�����ٶȵ�У����ʱ��Ϊ8��![]() =
=![]() �����ӣ���
�����ӣ���
30-![]() =
=![]() ��3.3�����ӣ���������ʵ������絽ѧУ3.3���ӣ�
��3.3�����ӣ���������ʵ������絽ѧУ3.3���ӣ�


 ����ѧ����ϵ�д�
����ѧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() �ڵڶ����ޣ�����
�ڵڶ����ޣ�����![]() ��
��![]() �����ʽ
�����ʽ![]() ����
����![]() �ڵ�һ�����ڣ�����
�ڵ�һ�����ڣ�����![]() ����
����![]() �ύ�ڵ�
�ύ�ڵ�![]() ��
��
��1����![]() ʱ����
ʱ����![]() ������ꣻ
������ꣻ
��2����![]() ��
��![]() ���ϴ�
���ϴ�![]() ������ÿ��1����λ���ȵ��ٶ����
������ÿ��1����λ���ȵ��ٶ����![]() �˶�������
�˶�������![]() ���ֹͣ�˶�������ʱ��Ϊ
���ֹͣ�˶�������ʱ��Ϊ![]() ��ʱ�������ǵ�
��ʱ�������ǵ�![]() ���
���![]() �غϵ��������
�غϵ��������![]() ��
��![]() ��
��![]() �Ĵ�С��ϵ��
�Ĵ�С��ϵ��
��3����ͼ����![]() ����
����![]() ������
������![]() ��һ���㣬
��һ���㣬![]() ��
��![]() ��ƽ���߽��ڵ�
��ƽ���߽��ڵ�![]() ��
��![]() �Ĵ�С�Ƿ����
�Ĵ�С�Ƿ����![]() ��λ�ñ仯�����ı䣬�����䣬�����
��λ�ñ仯�����ı䣬�����䣬�����![]() �Ķ��������ı䣬˵�����ɣ�
�Ķ��������ı䣬˵�����ɣ�



�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ��������ABC�У���ABC��90��.

(1)������ACB��ƽ���ߣ�������AB���ڵ�O�����Ե�OΪԲ�ģ�OBΪ�뾶����O(�߹���ͼ��������ͼ�ۼ�����д����)��
(2)֤����AC��������O�����ߣ�
(3)��BC��![]() ����A��30�������AOC�������
����A��30�������AOC�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס��������ֱ��A��B����ͬʱ����������ʻ�����ҳ�����A�غ�������ԭ����Զ��B�ķ�����ʻ�����׳�����B�غ�������ͷ��������ԭ�����ҳ�ͬ����ʻ������15Сʱ������ͬʱ�����A��300ǧ��C�أ���;��Ϣʱ����Բ��ƣ�����������ʻ��ʱ��Ϊx��Сʱ��������֮��ľ���Ϊy��ǧ�ף���y��x֮��ĺ�����ϵ��ͼ��ʾ���׳�����B��ʱ���ҳ���A��_____ǧ�ף�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ACΪ��O��ֱ����AC=4��B��D�ֱ���AC�����Բ�ϣ���BAD=60����BD��AC�Ľ���ΪE��

��1�����O��BD�ľ��뼰��OBD�Ķ�����
��2����DE=2BE����![]() ��ֵ��CD�ij���
��ֵ��CD�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,A,B,C������ͬһֱ����,�ֱ���AB,BC��AB>BC��Ϊ��,��ֱ��AC��ͬ�����ȱ���ABD�͵ȱ���BCE,����AE��BD�ڵ�M,����CD��BE�ڵ�N,����MN. ���½��ۣ���AE=DC����MN//AB����BD��AE���ܡ�DPM=60��������BMN�ǵȱ�������.������ȷ����__________����������ȷ����Ŷ����ϣ�.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������x�ķ���x2-ax+a2-3=0������һ����������ʵ��a��ȡֵ��Χ�ǣ�������
A. -2��a��2 B. ![]() ��a��2 C.
��a��2 C. ![]() ��a��2 D.
��a��2 D. ![]() ��a��2
��a��2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У���AB��AC�Ĵ�ֱƽ���߷ֱ�BC��D��E��
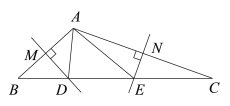
��1����BC=5������ADE���ܳ���
��2������BAD+��CAE=60�������BAC�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,A,B,C������ͬһֱ����,�ֱ���AB,BC��AB>BC��Ϊ��,��ֱ��AC��ͬ�����ȱ���ABD�͵ȱ���BCE,����AE��BD�ڵ�M,����CD��BE�ڵ�N,����MN. ���½��ۣ���AE=DC����MN//AB����BD��AE���ܡ�DPM=60��������BMN�ǵȱ�������.������ȷ����__________����������ȷ����Ŷ����ϣ�.

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com