
【题目】如图,A,B,C三点在同一直线上,分别以AB,BC(AB>BC)为边,在直线AC的同侧作等边ΔABD和等边ΔBCE,连接AE交BD于点M,连接CD交BE于点N,连接MN. 以下结论:①AE=DC,②MN//AB,③BD⊥AE,④∠DPM=60°,⑤ΔBMN是等边三角形.其中正确的是__________(把所有正确的序号都填上).

【答案】①②④⑤
【解析】
①由三角形ABD与三角形BCE都为等边三角形,利用等边三角形的性质得到两条边对应相等,两个角相等都为60°,利用SAS即可得到三角形ABE与三角形DBC全等即可得结论;
②由①中三角形ABE与三角形DBC全等,利用全等三角形的对应角相等得到一对角相等,再由∠ABD=∠EBC=60°,利用平角的定义得到∠MBE=∠NBC=60°,再由EB=CB,利用ASA可得出三角形EMB与三角形CNB全等,利用全等三角形的对应边相等得到MB=NB,再由∠MBE=60°,利用有一个角为60°的等腰三角形为等边三角形可得出三角形BMN为等边三角形;可得∠BMN=60°,进行可得∠BMN=∠ABD,故MN//AB,从而可判断②,⑤正确;
③无法证明PM=PN,因此不能得到BD⊥AE;
④由①得∠EAB=∠CDB,根据三角形内角和和外角的性质可证得结论.
①∵等边△ABD和等边△BCE,
∴AB=DB,BE=BC,∠ABD=∠EBC=60°,
∴∠ABE=∠DBC=120°,
在△ABE和△DBC中,
∵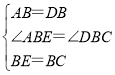 ,
,
∴△ABE≌△DBC(SAS),
∴AE=DC,
故①正确;
∵△ABE≌△DBC,
∴∠AEB=∠DCB,
又∠ABD=∠EBC=60°,
∴∠MBE=180°-60°-60°=60°,
即∠MBE=∠NBC=60°,
在△MBE和△NBC中,
∵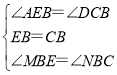 ,
,
∴△MBE≌△NBC(ASA),
∴BM=BN,∠MBE=60°,
则△BMN为等边三角形,
故⑤正确;
∵△BMN为等边三角形,
∴∠BMN=60°,
∵∠ABD=60°,
∴∠BMN=∠ABD,
∴MN//AB,
故②正确;
③无法证明PM=PN,因此不能得到BD⊥AE;
④由①得∠EAB=∠CDB,∠APC+∠PAC+∠PCA=180°,
∴∠PAC+∠PCA=∠PDB+∠PCB=∠DBA=60°,
∵∠DPM =∠PAC+∠PCA
∴∠DPM =60°,故④正确,
故答案为:①②④⑤.


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:初中数学 来源: 题型:
【题目】作出函数y=2-2x的图象,并根据图象回答下列问题:
(1)y的值随x的增大而____,减小而____;
(2)图象与x轴的交点坐标是___;与y轴的交点坐标是____;
(3)函数y=2-2x的图象与坐标轴所围成的三角形的面积是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们用[a]表示不大于a的最大整数,例如:[2.5]=2,[3]=3,[-2.5]=-3;用<a>表示大于a的最小整数,例如:<2.5>=3,<3>=4,<-2.5>=-2.根据上述规定,解决下列问题:
(1)[-4.5]=______,<3.01>=____;
(2)若x为整数,且[x]+<x>=2 017,求x的值;
(3)若x,y满足方程组![]() ,求x,y的取值范围.
,求x,y的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD外取一点E,连接AE、BE、DE.过点A作AE的垂线交DE于点P.若AE=AP=1,PB=![]() .下列结论:①△APD≌△AEB;②点B到直线AE的距离为
.下列结论:①△APD≌△AEB;②点B到直线AE的距离为![]() ;③EB⊥ED;④S△APD+S△APB=1+
;③EB⊥ED;④S△APD+S△APB=1+![]() ;⑤S正方形ABCD=4+
;⑤S正方形ABCD=4+![]() .其中正确结论的序号是 .
.其中正确结论的序号是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小亮家距离学校8千米,昨天早晨,小亮骑车上学途中,自行车“爆胎”,恰好路边有“自行车”维修部,几分钟后车修好了,为了不迟到,他加快了骑车到校的速度.回校后,小亮根据这段经历画出如下图象.该图象描绘了小亮行的路程S与他所用的时间t之间的关系.请根据图象,解答下列问题:
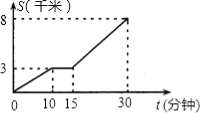
(1)小亮行了多少千米时,自行车“爆胎”?修车用了几分钟?
(2)小亮到校路上共用了多少时间?
(3)如果自行车没有“爆胎”,一直用修车前的速度行驶,那么他比实际情况早到或晚到学校多少分钟(精确到0.1)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D,E分别是AB,AC上的点,BE与CD交与点O,给出下列四个条件:①∠DBO=∠ECO,②∠BDO=∠CEO,③BD=CE,④OB=OC.
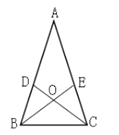
(1)从上述四个条件中,任选两个为条件,可以判定△ABC是等腰三角形?写出所有可能的情况.
(2)选择(1)中的某一种情形,进行说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在矩形ABCD中,AD=8,CD=4,点E从点D出发,沿线段DA以每秒1个单位长的速度向点A方向移动,到达A点停止运动;同时点F从点C出发,沿射线CD方向以每秒2个单位长的速度移动,到达D点停止运动,设点E移动的时间为t(秒).
(1)当t=1时,求四边形BCFE的面积;
(2)设四边形BCFE的面积为S,求S与t之间的关系式,并写出t的取值范围;
(3)若F点到达D点后立即返回,并在线段CD上往返运动,当E点到达A点时它们同时停止运动,求当t为何值时,以E,F,D三点为顶点的三角形是等腰三角形,并求出此的等腰三角形的面积S△EDF.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电信公司手机的A类收费标准如下:不管通话时间多长,每部手机每月必须缴月租费12元,另外,通话费按![]() 元
元![]() 计;B类收费标准如下:没有月租费,但通话费按
计;B类收费标准如下:没有月租费,但通话费按![]() 元
元![]() 计
计![]() 按照此类收费标准完成下列各题:
按照此类收费标准完成下列各题:
![]() 直接写出每月应缴费用
直接写出每月应缴费用![]() 元
元![]() 与通话时长
与通话时长![]() 分
分![]() 之间的关系式:
之间的关系式:
A类:______B类:______
![]() 若每月平均通话时长为300分钟,选择______类收费方式较少.
若每月平均通话时长为300分钟,选择______类收费方式较少.
![]() 求每月通话多长时间时,按
求每月通话多长时间时,按![]() 两类收费标准缴费,所缴话费相等.
两类收费标准缴费,所缴话费相等.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读下列材料,再解答下列问题:
题:分解因式:![]()
解:将“![]() ”看成整体,设
”看成整体,设![]() ,则原式=
,则原式=![]()
![]()
再将“![]() ”还原,得原式=
”还原,得原式=![]() .
.
上述解题用到的是“整体思想”,“整体思想”是数学解题中常用的一种思想方法,请你仿照上面的方法解答下列问题:
(1)因式分解:![]() ;
;![]() .
.
(2)因式分解:![]() ;
;![]() .
.
(3)求证:若![]() 为正整数,则式子
为正整数,则式子![]() 的值一定是某一个正整数的平方.
的值一定是某一个正整数的平方.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com