
【题目】我们用[a]表示不大于a的最大整数,例如:[2.5]=2,[3]=3,[-2.5]=-3;用<a>表示大于a的最小整数,例如:<2.5>=3,<3>=4,<-2.5>=-2.根据上述规定,解决下列问题:
(1)[-4.5]=______,<3.01>=____;
(2)若x为整数,且[x]+<x>=2 017,求x的值;
(3)若x,y满足方程组![]() ,求x,y的取值范围.
,求x,y的取值范围.
【答案】(1) -5, 4;(2)x=1 008;(3)-1≤x<0,2≤y<3.
【解析】试题分析:(1)根据[a]表示不大于a的最大整数,<a>表示大于a的最小整数,进行计算即可;
(2)根据[x]+<x>=2017,可得![]() 进而得到
进而得到![]()
(3)解方程组可得![]() 根据[a]表示不大于a的最大整数,<a>表示大于a的最小整数,即可得到x、y的取值范围.
根据[a]表示不大于a的最大整数,<a>表示大于a的最小整数,即可得到x、y的取值范围.
试题解析: (1)由题可得[4.5]=5,<3.01>=4,
故答案为:5,4;
(2)∵[x]![]() x,且x为整数,
x,且x为整数,
∴[x]=x,
∵<x>>x,且x为整数,
∴<x>=x+1,
∵[x]+<x>=2017,
∴x+(x+1)=2017,
解得x=1008;
(3)解原方程组,得![]()
又∵[x]表示不大于x的最大整数,<x>表示大于x的最小整数,
![]()


科目:初中数学 来源: 题型:
【题目】某超市销售甲、乙两种糖果,购买3千克甲种糖果和1千克乙种糖果共需44元,购买1千克甲种糖果和2千克乙种糖果共需38元.
(1)求甲、乙两种糖果的价格;
(2)若购买甲、乙两种糖果共20千克,且总价不超过240元,问甲种糖果最少购买多少千克?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,M为BC边上的中点,D是射线AM上的一个动点,以CD为一边且在CD的下方作等边△CDE,连接BE. 
(1)填空:若D与M重合时(如图1)∠CBE=度;
(2)如图2,当点D在线段AM上时(点D不与A、M重合),请判断(1)中结论是否成立?并说明理由;
(3)在(1)的条件下,若AB=6,试求CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC的三个顶点的坐标分别为A(﹣5,3)、B(﹣2,﹣2)、C(﹣3,4). 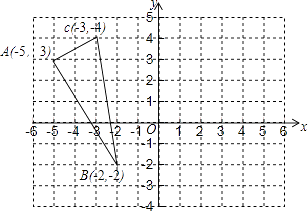
(1)作出△ABC关于y轴对称的△A1B1C1;
(2)写出点A关于x轴对称的点A2的坐标;
(3)△ABC的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
小聪遇到这样一个有关角平分线的问题:如图1,在△ABC中,∠A=2∠B,CD平分∠ACB,AD=2.2,AC=3.6
求BC的长.
小聪思考:因为CD平分∠ACB,所以可在BC边上取点E,使EC=AC,连接DE.这样很容易得到△DEC≌△DAC,经过推理能使问题得到解决(如图2).
请回答: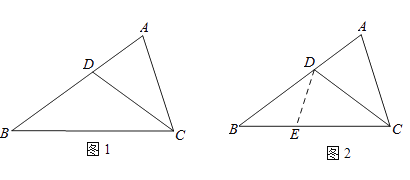
(1)△BDE是
(2)BC的长为
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了抓住市文化艺术节的商机,某商店决定购进A,B两种艺术节纪念品.若购进A种纪念品8件,B种纪念品3件,需要950元;若购进A种纪念品5件,
B种纪念品6件,需要800元.
(1)求购进A,B两种纪念品每件各需多少元?
(2)若该商店决定购进这两种纪念品共100件,考虑市场需求和资金周转,用于购买这100件纪念品的资金不少于7500元,但不超过7650元,那么该商店共有几种进货方案?
(3)若销售每件A种纪念品可获利润20元,每件B种纪念品可获利润30元,在(2)问的各种进货方案中,哪一种方案获利最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠CAB=∠DAB,则添加下列一个条件不能使△ABC≌△ABD的是( ) 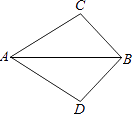
A.AC=AD
B.BC=BD
C.∠C=∠D
D.∠ABC=∠ABD
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com