
【题目】阅读下面材料:
小聪遇到这样一个有关角平分线的问题:如图1,在△ABC中,∠A=2∠B,CD平分∠ACB,AD=2.2,AC=3.6
求BC的长.
小聪思考:因为CD平分∠ACB,所以可在BC边上取点E,使EC=AC,连接DE.这样很容易得到△DEC≌△DAC,经过推理能使问题得到解决(如图2).
请回答: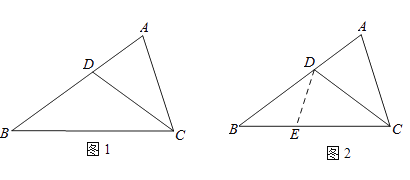
(1)△BDE是
(2)BC的长为
【答案】
(1)等腰三角形
(2)5.8
【解析】解:(1)△BDE是等腰三角形,
在△ACD与△ECD中, 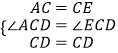 ,
,
∴△ACD≌△ECD,
∴AD=DE,∠A=∠DEC,
∵∠A=2∠B,
∴∠DEC=2∠B,
∴∠B=∠EDB,
∴△BDE是等腰三角形;(2)BC的长为5.8,
∵△ABC中,AB=AC,∠A=20°,
∴∠ABC=∠C=80°,
∵BD平分∠B,
∴∠1=∠2=40°∠BDC=60°,
在BA边上取点E,使BE=BC=2,连接DE,
则△DEB≌△DBC,∴∠BED=∠C=80°,
∴∠4=60°,
∴∠3=60°,
在DA边上取点F,使DF=DB,连接FE,
则△BDE≌△FDE,
∴∠5=∠1=40°,BE=EF=2,
∵∠A=20°,
∴∠6=20°,
∴AF=EF=2,
∵BD=DF=2.3,
∴AD=BD+BC=4.3.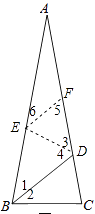


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
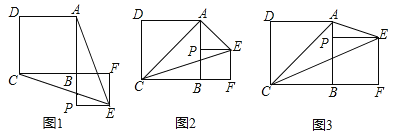
【题目】已知正方形ABCD,P为射线AB上的一点,以BP为边作正方形BPEF,使点F在线段CB的延长线上,连接EA、EC.
(1)如图1,若点P在线段AB的延长线上,求证:EA=EC;
(2)若点P在线段AB上.
①如图2,连接AC,当P为AB的中点时,判断△ACE的形状,并说明理由;
②如图3,设AB=a,BP=b,当EP平分∠AEC时,求a:b及∠AEC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校举行全体学生“汉字听写”比赛,每位学生听写汉字![]() 个.随机抽取了部分学生的听写结果,绘制成如下的图表:
个.随机抽取了部分学生的听写结果,绘制成如下的图表:
组别 | 正确字数 | 人数 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
根据以上信息完成下列问题:
(![]() )统计表中的
)统计表中的![]() __________,
__________,![]() __________,并补全直方图.
__________,并补全直方图.
(![]() )扇形统计图中“
)扇形统计图中“![]() 组”所对应的圆心角的度数是__________.
组”所对应的圆心角的度数是__________.
(![]() )已知该校共有
)已知该校共有![]() 名学生,如果听写正确的字的个数少于
名学生,如果听写正确的字的个数少于![]() 个定为不合格,请你估计该校本次听写比赛不合格的学生人数.
个定为不合格,请你估计该校本次听写比赛不合格的学生人数.
各组别人数分布比例 | |
|
|
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们用[a]表示不大于a的最大整数,例如:[2.5]=2,[3]=3,[-2.5]=-3;用<a>表示大于a的最小整数,例如:<2.5>=3,<3>=4,<-2.5>=-2.根据上述规定,解决下列问题:
(1)[-4.5]=______,<3.01>=____;
(2)若x为整数,且[x]+<x>=2 017,求x的值;
(3)若x,y满足方程组![]() ,求x,y的取值范围.
,求x,y的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“抢红包”是2015年春节十分火爆的一项网络活动,某企业有4000名职工,从中随机抽取350人,按年龄分布和“抢红包”所持态度情况进行调查,并将调查结果绘成了条形统计图和扇形统计图.
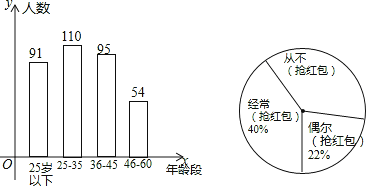
(1)这次调查中,如果职工年龄的中位数是整数,那么这个中位数所在的年龄段是哪一段?
(2)如果把对“抢红包”所持态度中的“经常(抢红包)”和“偶尔(抢红包)”统称为“参与抢红包”,那么这次接受调查的职工中“参与抢红包”的人数是多少?并估计该企业“从不(抢红包)”的人数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
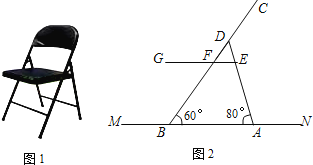
【题目】如图1是一把折叠椅子,图2是椅子完全打开支稳后的侧面示意图,其中AD和BC表示两根较粗的钢管,EG表示座板平面,EG和BC相交于点F,MN表示地面所在的直线,EG∥MN,EG距MN的高度为42cm,AB=43cm,CF=42cm,∠DBA=60°,∠DAB=80°.求两根较粗钢管AD和BC的长.(结果精确到0.1cm.参考数据:sin80°≈0.98,cos80°≈0.17,tan80°≈5.67,sin60°≈0.87,cos60°≈0.5,tan60°≈1.73)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com