
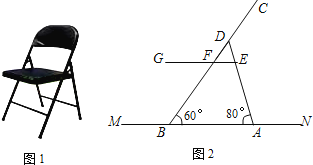
【题目】如图1是一把折叠椅子,图2是椅子完全打开支稳后的侧面示意图,其中AD和BC表示两根较粗的钢管,EG表示座板平面,EG和BC相交于点F,MN表示地面所在的直线,EG∥MN,EG距MN的高度为42cm,AB=43cm,CF=42cm,∠DBA=60°,∠DAB=80°.求两根较粗钢管AD和BC的长.(结果精确到0.1cm.参考数据:sin80°≈0.98,cos80°≈0.17,tan80°≈5.67,sin60°≈0.87,cos60°≈0.5,tan60°≈1.73)
【答案】两根较粗钢管AD和BC的长分别为58.2cm、90.3cm.
【解析】试题分析:作FH⊥AB于H,DQ⊥AB于Q,如图2,FH=42cm,先在Rt△BFH中,利用∠FBH的正弦计算出BF≈48.28,则BC=BF+CF=≈90.3(cm),再分别在Rt△BDQ和Rt△ADQ中,利用正切定义用DQ表示出BQ和AQ,得BQ=![]() ,AQ=
,AQ=![]() ,则利用BQ+AQ=AB=43得到
,则利用BQ+AQ=AB=43得到![]() +
+![]() =43,解得DQ≈56.999,然后在Rt△ADQ中,利用sin∠DAQ的正弦可求出AD的长.
=43,解得DQ≈56.999,然后在Rt△ADQ中,利用sin∠DAQ的正弦可求出AD的长.
试题解析:
在Rt△BFH中,作FH⊥AB于H,DQ⊥AB于Q,如图2,FH=42cm,
∵sin∠FBH=![]() ,
,
∴BF=![]() ≈48.28,
≈48.28,
∴BC=BF+CF=48.28+42≈90.3(cm);
在Rt△BDQ中,∵tan∠DBQ=![]() ,
,
∴BQ=![]() ,
,
在Rt△ADQ中,∵tan∠DAQ=![]() ,
,
∴AQ=![]() ,
,
∵BQ+AQ=AB=43,
∴![]() +
+![]() =43,解得DQ≈56.999,
=43,解得DQ≈56.999,
在Rt△ADQ中,∵sin∠DAQ=![]() ,
,
∴AD=![]() ≈58.2(cm).
≈58.2(cm).
答:两根较粗钢管AD和BC的长分别为58.2cm、90.3cm.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:
【题目】阅读下面材料:
小聪遇到这样一个有关角平分线的问题:如图1,在△ABC中,∠A=2∠B,CD平分∠ACB,AD=2.2,AC=3.6
求BC的长.
小聪思考:因为CD平分∠ACB,所以可在BC边上取点E,使EC=AC,连接DE.这样很容易得到△DEC≌△DAC,经过推理能使问题得到解决(如图2).
请回答: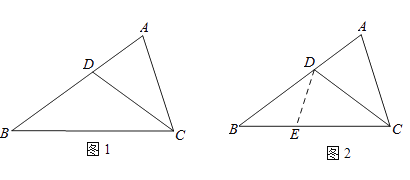
(1)△BDE是
(2)BC的长为
查看答案和解析>>
科目:初中数学 来源: 题型:
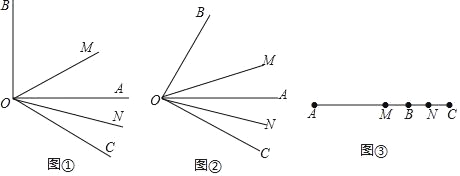
【题目】理解计算:如图①,∠AOB=90°,∠AOC为∠AOB外的一个角,且∠AOC=30°,射线OM平分∠BOC,ON平分∠AOC.求∠MON的度数;
拓展探究:如图②,∠AOB=α,∠AOC=β.(α,β为锐角),射线OM平分∠BOC,ON平分∠AOC.求∠MON的度数;
迁移应用:其实线段的计算与角的计算存在着紧密的联系,如图③线段AB=m,延长线段AB到C,使得BC=n,点M,N分别为AC,BC的中点,则MN的长为_____(直接写出结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】操作:
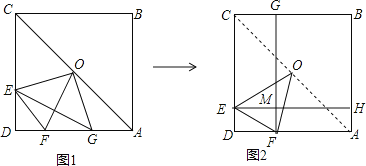
如图1,正方形ABCD中,AB=a,点E是CD边上一个动点,在AD上截取AG=DE,连接EG,过正方形的中线O作OF⊥EG交AD边于F,连接OE、OG、EF、AC.
探究:
在点E的运动过程中:
(1)猜想线段OE与OG的数量关系?并证明你的结论;
(2)∠EOF的度数会发生变化吗?若不会,求出其度数,若会,请说明理由.
应用:
(3)当a=6时,试求出△DEF的周长,并写出DE的取值范围;
(4)当a的值不确定时:
①若![]() =
=![]() 时,试求
时,试求![]() 的值;
的值;
②在图1中,过点E作EH⊥AB于H,过点F作FG⊥CB于G,EH与FG相交于点M;并将图1简化得到图2,记矩形MHBG的面积为S,试用含a的代数式表示出S的值,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com