
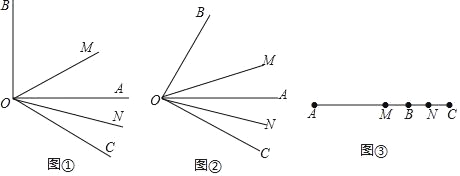
����Ŀ��������㣺��ͼ������AOB=90������AOCΪ��AOB���һ���ǣ��ҡ�AOC=30��������OMƽ�֡�BOC��ONƽ�֡�AOC�����MON�Ķ�����
��չ̽������ͼ������AOB=������AOC=������������Ϊ��ǣ�������OMƽ�֡�BOC��ONƽ�֡�AOC�����MON�Ķ�����
Ǩ��Ӧ�ã���ʵ�߶εļ�����ǵļ�������Ž��ܵ���ϵ����ͼ���߶�AB=m���ӳ��߶�AB��C��ʹ��BC=n����M��N�ֱ�ΪAC��BC���е㣬��MN�ij�Ϊ_____��ֱ��д���������
���𰸡�������㣺 ![]() ����չ̽����
����չ̽���� ![]() ��Ǩ��Ӧ�ã�
��Ǩ��Ӧ�ã� ![]() .
.
�����������������������㣺���ݽǵ�ƽ���ߵ��ص㣬���Ե�֪����������ȣ�����ԭ�ǵ�һ�룬���ݽ����֮���������ϵ���ɵó����ۣ�
��չ̽�������ݽǵ�ƽ���ߵ��ص㣬���Ե�֪����������ȣ�����ԭ�ǵ�һ�룬���ݽ����֮���������ϵ���ɵó����ۣ�
Ǩ��Ӧ�ã��������������ԭ����ͨ���Ƶ�����ֱ�ӣ��ó����ۣ�
���������������㣺�ߡ�BOC=��AOB+��AOC=90��+30��=120����
����OMƽ�֡�BOC��
���COM=![]() ��BOC=
��BOC=![]() ��120��=60����
��120��=60����
��ONƽ�֡�AOC��
���CON=![]() ��AOC=
��AOC=![]() ��30��=15����
��30��=15����
���MON=��COM����CON=60�㩁15��=45����
��չ̽�����ߡ�BOC=��AOB+��AOC=��+����
������OMƽ�֡�BOC��
���COM=![]() ��BOC=
��BOC=![]() ����+������
����+������
��ONƽ�֡�AOC��
���CON=![]() ��AOC=
��AOC=![]() ����
����
���MON=��COM����CON=![]() ����+������
����+������![]() ��=
��=![]() ����
����
Ǩ��Ӧ�ã���AB=m��BC=n��
��AC=AB+BC=m+n��
�ߵ�M��N�ֱ�ΪAC��BC���е㣬
��CM=![]() AC=
AC=![]() ��m+n����CN=
��m+n����CN=![]() BC=
BC=![]() n��
n��
��MN=CM��CN=![]() m��
m��
�ʴ�Ϊ�� ![]() m��
m��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����м�����ȷ���ǣ� ��
A.a+2a=3a2
B.aa2=a3
C.��2a��2=2a2
D.����a2��3=a6
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������������2015�괺��ʮ�ֻ𱬵�һ��������ij��ҵ��4000��ְ�������������ȡ350�ˣ�������ֲ����������������̬��������е��飬�������������������ͳ��ͼ������ͳ��ͼ��
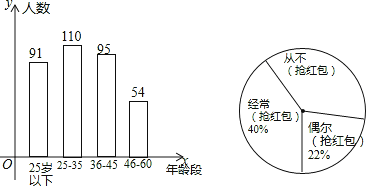
��1����ε����У����ְ���������λ������������ô�����λ�����ڵ����������һ�Σ�
��2������Ѷ��������������̬���е����������������������ż�������������ͳ��Ϊ�����������������ô��ν��ܵ����ְ������������������������Ƕ��٣������Ƹ���ҵ���Ӳ�������������������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
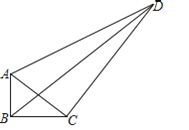
����Ŀ����ͼ�����ı���ABCD�У���ABC=90�㣬AB=3��BC=4��CD=10��DA=![]() �������н��ۣ���AC��BD����AC��CD����tan��DAC=2�����ı���ABCD�����Ϊ31����BD=2
�������н��ۣ���AC��BD����AC��CD����tan��DAC=2�����ı���ABCD�����Ϊ31����BD=2![]() ����ȷ����_______��
����ȷ����_______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������¼��У�������¼�����( )
A.���⻭����ֱ�������Σ�����������������B.���������εĶ�Ӧ�����
C.��O�İ뾶Ϊ5��OP��3����P�ڡ�O��D.ֱ�����Ե�Բ�ܽ�Ϊֱ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
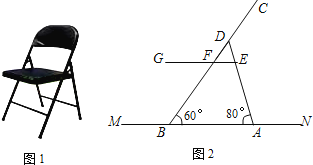
����Ŀ����ͼ1��һ���۵����ӣ�ͼ2��������ȫ��֧�Ⱥ�IJ���ʾ��ͼ������AD��BC��ʾ�����ϴֵĸֹܣ�EG��ʾ����ƽ�棬EG��BC�ཻ�ڵ�F��MN��ʾ�������ڵ�ֱ�ߣ�EG��MN��EG��MN�ĸ߶�Ϊ42cm��AB=43cm��CF=42cm����DBA=60�㣬��DAB=80�㣮�������ϴָֹ�AD��BC�ij����������ȷ��0.1cm���ο����ݣ�sin80���0.98��cos80���0.17��tan80���5.67��sin60���0.87��cos60���0.5��tan60���1.73��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ���ڡ�ABC����ADE�У���BAC=��DAE=90�㣬AB=AC��AD=AE����C��D��E������ͬһֱ���ϣ�����BD�� 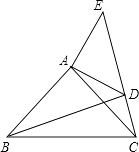
��֤��
��1����BAD�ա�CAE��
��2���Բ���BD��CE�к�����λ�ù�ϵ����֤����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com