
【题目】如图,在四边形ABCD中,∠ABC=90°,AB=3,BC=4,CD=10,DA=![]() ,则下列结论:①AC⊥BD;②AC⊥CD;③tan∠DAC=2;④四边形ABCD的面积为31;⑤BD=2
,则下列结论:①AC⊥BD;②AC⊥CD;③tan∠DAC=2;④四边形ABCD的面积为31;⑤BD=2![]() .正确的是_______.
.正确的是_______.
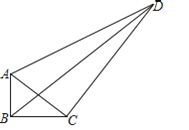
【答案】②③④⑤
【解析】∵∠ABC=90°,AB=3,BC=4,
∴AC=![]() =5,
=5,
在△ACD中,∵CD=10,DA=![]() ,
,
∴AC+CD=25+100=125=DA,
∴∠ACD=90°,即AC⊥CD,故①错误,②正确;
在Rt△ACD中,tan∠DAC=![]() =
=![]() =2,故③正确;
=2,故③正确;
S四边形ABCD=![]() =
=![]() ABBC+
ABBC+![]() ACCD=
ACCD=![]() ×3×4+
×3×4+![]() ×5×10=31,
×5×10=31,
故④正确;
作DM⊥BC,交BC延长线于M,如图所示:
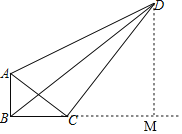
则∠M=90°,
∴∠DCM+∠CDM=90°,
∵∠ABC=90°,AB=3,BC=4,
∴AC=AB+BC=25,
∵CD=10,AD=![]() ,
,
∴AC+CD=AD,
∴△ACD是直角三角形,∠ACD=90°,
∴∠ACB+∠DCM=90°,
∴∠ACB=∠CDM,
∵∠ABC=∠M=90°,
∴△ABC∽△CMD,
∴![]() ,
,
∴CM=2AB=6,DM=2BC=8,
∴BM=BC+CM=10,
∴BD=![]() =
=![]() ,故⑤正确;
,故⑤正确;
故答案为:②③④⑤.


科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,M为BC边上的中点,D是射线AM上的一个动点,以CD为一边且在CD的下方作等边△CDE,连接BE. 
(1)填空:若D与M重合时(如图1)∠CBE=度;
(2)如图2,当点D在线段AM上时(点D不与A、M重合),请判断(1)中结论是否成立?并说明理由;
(3)在(1)的条件下,若AB=6,试求CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了抓住市文化艺术节的商机,某商店决定购进A,B两种艺术节纪念品.若购进A种纪念品8件,B种纪念品3件,需要950元;若购进A种纪念品5件,
B种纪念品6件,需要800元.
(1)求购进A,B两种纪念品每件各需多少元?
(2)若该商店决定购进这两种纪念品共100件,考虑市场需求和资金周转,用于购买这100件纪念品的资金不少于7500元,但不超过7650元,那么该商店共有几种进货方案?
(3)若销售每件A种纪念品可获利润20元,每件B种纪念品可获利润30元,在(2)问的各种进货方案中,哪一种方案获利最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠CAB=∠DAB,则添加下列一个条件不能使△ABC≌△ABD的是( ) 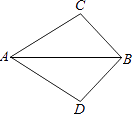
A.AC=AD
B.BC=BD
C.∠C=∠D
D.∠ABC=∠ABD
查看答案和解析>>
科目:初中数学 来源: 题型:
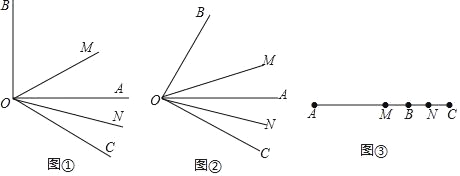
【题目】理解计算:如图①,∠AOB=90°,∠AOC为∠AOB外的一个角,且∠AOC=30°,射线OM平分∠BOC,ON平分∠AOC.求∠MON的度数;
拓展探究:如图②,∠AOB=α,∠AOC=β.(α,β为锐角),射线OM平分∠BOC,ON平分∠AOC.求∠MON的度数;
迁移应用:其实线段的计算与角的计算存在着紧密的联系,如图③线段AB=m,延长线段AB到C,使得BC=n,点M,N分别为AC,BC的中点,则MN的长为_____(直接写出结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】被历代数学家尊为“算经之首”的《九章算术》是中国古代算法的扛鼎之作.《九章算术》中记载:“今有五雀、六燕,集称之衡,雀俱重,燕俱轻.一雀一燕交而处,衡适平.并燕、雀重一斤.问燕、雀一枚各重几何?”
译文:“今有![]() 只雀、
只雀、![]() 只燕,分别聚焦而且用衡器称之,聚在一起的雀重,燕轻.经一只雀、一只燕交换位置而放,重量相等.
只燕,分别聚焦而且用衡器称之,聚在一起的雀重,燕轻.经一只雀、一只燕交换位置而放,重量相等.![]() 只雀、
只雀、![]() 只燕重量为
只燕重量为![]() 斤.问雀、燕每
斤.问雀、燕每![]() 只各重多少斤?”
只各重多少斤?”
请列方程组解答上面的问题.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一副三角板按如图放置,则下列结论:
①如果∠2=30°,则有AC∥DE;
②∠BAE+∠CAD =180°;
③如果BC∥AD,则有∠2=45°;
④如果∠CAD=150°,必有∠4=∠C;
正确的有( )
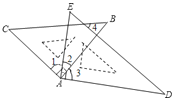
A. ①②③ B. ①②④ C. ①③④ D. ①②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com