
【题目】已知:如图,在△ABC、△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C、D、E三点在同一直线上,连接BD. 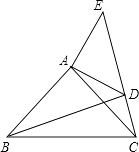
求证:
(1)△BAD≌△CAE;
(2)试猜想BD、CE有何特殊位置关系,并证明.
【答案】
(1)证明:∵∠BAC=∠DAE=90°
∴∠BAC+∠CAD=∠DAE+CAD
即∠BAD=∠CAE,
又∵AB=AC,AD=AE,
∴△BAD≌△CAE(SAS)
(2)证明:BD、CE特殊位置关系为BD⊥CE.
证明如下:由(1)知△BAD≌△CAE,
∴∠ADB=∠E.
∵∠DAE=90°,
∴∠E+∠ADE=90°.
∴∠ADB+∠ADE=90°.
即∠BDE=90°.
∴BD、CE特殊位置关系为BD⊥CE
【解析】要证(1)△BAD≌△CAE,现有AB=AC,AD=AE,需它们的夹角∠BAD=∠CAE,而由∠BAC=∠DAE=90°很易证得.(2)BD、CE有何特殊位置关系,从图形上可看出是垂直关系,可向这方面努力.要证BD⊥CE,需证∠BDE=90°,需证∠ADB+∠ADE=90°可由直角三角形提供.


 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:初中数学 来源: 题型:
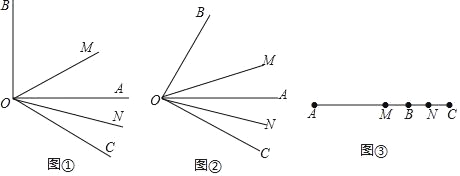
【题目】理解计算:如图①,∠AOB=90°,∠AOC为∠AOB外的一个角,且∠AOC=30°,射线OM平分∠BOC,ON平分∠AOC.求∠MON的度数;
拓展探究:如图②,∠AOB=α,∠AOC=β.(α,β为锐角),射线OM平分∠BOC,ON平分∠AOC.求∠MON的度数;
迁移应用:其实线段的计算与角的计算存在着紧密的联系,如图③线段AB=m,延长线段AB到C,使得BC=n,点M,N分别为AC,BC的中点,则MN的长为_____(直接写出结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
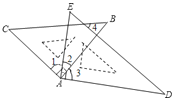
【题目】将一副三角板按如图放置,则下列结论:
①如果∠2=30°,则有AC∥DE;
②∠BAE+∠CAD =180°;
③如果BC∥AD,则有∠2=45°;
④如果∠CAD=150°,必有∠4=∠C;
正确的有( )
A. ①②③ B. ①②④ C. ①③④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)(﹣3a2b3)2(﹣a3b2)5÷a2b4;
(2)( ![]() )2012×(﹣1.5)2013÷(﹣1)2014;
)2012×(﹣1.5)2013÷(﹣1)2014;
(3)[x(x2y2﹣xy)﹣y(x2﹣x3y)]÷3x2y;
(4)(5x+7y﹣3)(5x﹣7y+3);
(5)(a+2b﹣c)2;
(6)(x+2y)2(x﹣2y)2 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图2的形状拼成一个正方形. 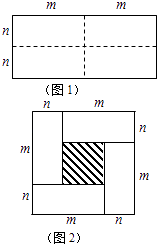
(1)请写出图2中阴影部分的面积:;
(2)观察图2你能写出下列三个代数式之间的等量关系吗?代数式:(m+n)2 , (m﹣n)2 , mn.;
(3)根据(2)中的等量关系,解决如下问题:若a+b=7,ab=5,求a﹣b的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com