
【题目】平面直角坐标系xOy中,点A、B的横坐标分别为a、![]() ,二次函数
,二次函数![]() 的图象经过点A、B,且a、m满足
的图象经过点A、B,且a、m满足![]() 为常数
为常数![]() .
.
![]() 若一次函数
若一次函数![]() 的图象经过A、B两点.
的图象经过A、B两点.
![]() 当
当![]() 、
、![]() 时,求k的值;
时,求k的值;
![]() 若y随x的增大而减小,求d的取值范围;
若y随x的增大而减小,求d的取值范围;
![]() 当
当![]() 且
且![]() 、
、![]() 时,判断直线AB与x轴的位置关系,并说明理由;
时,判断直线AB与x轴的位置关系,并说明理由;
![]() 点A、B的位置随着a的变化而变化,设点A、B运动的路线与y轴分别相交于点C、D,线段CD的长度会发生变化吗?如果不变,求出CD的长;如果变化,请说明理由.
点A、B的位置随着a的变化而变化,设点A、B运动的路线与y轴分别相交于点C、D,线段CD的长度会发生变化吗?如果不变,求出CD的长;如果变化,请说明理由.
【答案】(1)![]() k的值为
k的值为![]() ;
;![]() 的取值范围为
的取值范围为![]() ;(2)
;(2)![]() 轴;
轴;![]() 线段CD的长度不变,理由见解析.
线段CD的长度不变,理由见解析.
【解析】
(1)①当a=1、d=-1时,m=2a-d=3,于是得到抛物线的解析式,然后求得点A和点B的坐标,最后将点A和点B的坐标代入直线AB的解析式求得k的值即可;
②将x=a,x=a+2代入抛物线的解析式可求得点A和点B的纵坐标,然后依据y1随着x的增大而减小,可得到-(a-m)(a+2)>-(a+2-m)(a+4),结合已知条件2a-m=d,可求得d的取值范围;
(2)由d=-4可得到m=2a+4,则抛物线的解析式为y=-x2+(2a+2)x+4a+8,然后将x=a、x=a+2代入抛物线的解析式可求得点A和点B的纵坐标,最后依据点A和点B的纵坐标可判断出AB与x轴的位置关系;
(3)先求得点A和点B的坐标,于是得到点A和点B运动的路线与字母a的函数关系式,则点C(0,-2d),D(0,-2d-8),于是可得到CD的长度.
![]() 当
当![]() 、
、![]() 时,
时,![]() ,
,
所以二次函数的表达式是![]() .
.
![]() ,
,
![]() 点A的横坐标为1,点B的横坐标为3,
点A的横坐标为1,点B的横坐标为3,
把![]() 代入抛物线的解析式得:
代入抛物线的解析式得:![]() ,把
,把![]() 代入抛物线的解析式得:
代入抛物线的解析式得:![]() ,
,
![]() ,
,![]() .
.
将点A和点B的坐标代入直线的解析式得:![]() ,解得:
,解得:![]() ,
,
所以k的值为![]() .
.
![]() ,
,
![]() 当
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,
,
![]() 随着x的增大而减小,且
随着x的增大而减小,且![]() ,
,
![]() ,解得:
,解得:![]() ,
,
又![]() ,
,
![]() 的取值范围为
的取值范围为![]() .
.
![]() 且
且![]() 、
、![]() ,
,![]() ,
,
![]() .
.
![]() 二次函数的关系式为
二次函数的关系式为![]() .
.
把![]() 代入抛物线的解析式得:
代入抛物线的解析式得:![]() .
.
把![]() 代入抛物线的解析式得:
代入抛物线的解析式得:![]() .
.
![]() 、
、![]() .
.
![]() 点A、点B的纵坐标相同,
点A、点B的纵坐标相同,
![]() 轴.
轴.
![]() 线段CD的长度不变.
线段CD的长度不变.
![]() 过点A、点B,
过点A、点B,![]() ,
,
![]() .
.
![]() ,
,![]() .
.
![]() 把
把![]() 代入
代入![]() ,得:
,得:![]() ,
,
![]() .
.
![]() 点D在y轴上,即
点D在y轴上,即![]() ,
,
![]() ,.
,.
把![]() 代入
代入![]() 得:
得:![]() .
.
![]() .
.
![]() .
.
![]() 线段CD的长度不变.
线段CD的长度不变.


科目:初中数学 来源: 题型:
【题目】如图①,△ABC中,AB=AC,∠B、∠C的平分线交于O点,过O点作EF∥BC交AB、AC于E、F.试回答:

(1)图中等腰三角形是 .猜想:EF与BE、CF之间的关系是 .理由:
(2)如图②,若AB≠AC,图中等腰三角形是 .在第(1)问中EF与BE、CF间的关系还存在吗?
(3)如图③,若△ABC中∠B的平分线BO与三角形外角平分线CO交于O,过O点作OE∥BC交AB于E,交AC于F.这时图中还有等腰三角形吗?EF与BE、CF关系又如何?说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
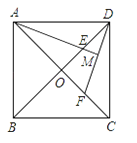
【题目】(8分)如图,在正方形ABCD中,对角线AC、BD相交于O,E、F分别在OD、OC上,且DE=CF,连结DF、AE,AE的延长线交于DF于点M,求证:AM⊥DF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校决定加强羽毛球、篮球、乒乓球、排球、足球五项球类运动,每位同学必须且只能选择一项球类运动,对该校学生随机抽取![]() 进行调查,根据调查结果绘制了如下不完整的频数分布表和扇形统计图:
进行调查,根据调查结果绘制了如下不完整的频数分布表和扇形统计图:
运动项目 | 频数(人数) |
羽毛球 | 30 |
篮球 |
|
乒乓球 | 36 |
排球 |
|
足球 | 12 |

请根据以上图表信息解答下列问题:
(1)频数分布表中的![]() ,
,![]() ;
;
(2)在扇形统计图中,“排球”所在的扇形的圆心角为 度;
(3)全校有多少名学生选择参加乒乓球运动?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中.

(1)若点E、F分别在AB、AD上,且AE=DF.试判断DE与CF的数量及位置关系,并说明理由;
(2)若P、Q、M、N是正方形ABCD各边上的点,PQ与MN相交,且PQ=MN,问PQ⊥MN成立吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC和∠ACB的平分线相交于点G,过点G作EF∥BC交AB于E,交AC于F,过点G作GD⊥AC于D,下列三个结论:① EF=BE+CF;②∠BGC=90°+![]() ∠A;③点G到△ABC各边的距离相等;其中正确的结论有_________(填序号)
∠A;③点G到△ABC各边的距离相等;其中正确的结论有_________(填序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中,AB=AC,CD是∠ACB的平分线,DE∥BC,交AC于点 E.

(1)求证:DE=CE.
(2)若∠CDE=25°,求∠A 的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC=5,线段AB的垂直平分线DE分别交边AB、AC于点E、D.

(1)若∠A=40°,求∠DBC的度数;
(2)若△BCD的周长为8,求BC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com