【题目】如图所示，已知在
中，BE平分
交AC于点E，
交AB于点D，
，则
的度数为________．
【答案】
【解析】
由已知条件只能得到∠ACD=90°，由三角形外角性质可知∠BEA=∠ACD+∠BCD+∠CBE，因此求出∠BCD+∠CBE的度数即可得到答案；由垂直的定义及三角形内角和定理易得∠A+∠ABC+∠BCD=90°，结合角平分线的概念及∠BCD=∠A即可得到∠BCD+∠CBE的度数，进而可对题目进行解答.
∵CD⊥AC，
∴∠ACD=90°，
∴∠A+∠ABC+∠BCD=180°-∠ACD=90°.
∵BE平分∠ABC，
∴∠ABC=2∠CBE.
∵∠BCD=∠A，
∴∠A+∠ABC+∠BCD=2∠BCD+2∠CBE=90°，
∴∠BCD+∠CBE=45°，
∴∠BEA=∠ACD+∠BCD+∠CBE=135°.
故答案为：．
天天向上一本好卷系列答案
小学生10分钟应用题系列答案科目：初中数学 来源： 题型：
【题目】平面直角坐标系xOy中，点A、B的横坐标分别为a、
，二次函数
的图象经过点A、B，且a、m满足
为常数
．
若一次函数
的图象经过A、B两点．
当
、
时，求k的值；
若y随x的增大而减小，求d的取值范围；
当
且
、
时，判断直线AB与x轴的位置关系，并说明理由；
点A、B的位置随着a的变化而变化，设点A、B运动的路线与y轴分别相交于点C、D，线段CD的长度会发生变化吗？如果不变，求出CD的长；如果变化，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知，在
中，
，
，
，D是AC边上的一个动点，将
沿BD所在直线折叠，使点A落在点E处．
如图
，若点D是AC的中点，连接
求证：四边形BCED是平行四边形；
如图
，若
，求
的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】小王抽样调查了本地若干天的空气质量情况，把空气质量分成四类：
类，
类，
类和
类，分别对应的质量级别为优、良、轻度污染和中度污染四种情况，并绘制两个统计图（部分信息缺失）；
空气质量条形统计图
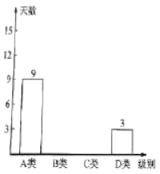
空气质量扇形统计图
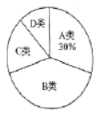
（1）本次调查的样本容量是________；
（2）已知类和类在扇形统计图中所占的夹角为
度，类的频数是类的
倍，通过计算，求出类和类的频数，并完成条形统计图；
（3）计算类在扇形统计图中所对应的圆心角度数；
（4）若一年按
天计算，求本地全年空气质量达到优良以上的天数（保留整数）．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某工程队用甲、乙两台隧道挖掘机从两个方向挖掘同一条隧道，因为地质条件不同，甲、乙的挖掘速度不同，已知甲、乙同时挖掘
天，可以挖
米，若甲挖
天，乙挖
天可以挖掘
米．
（1）请问甲、乙挖掘机每天可以挖掘多少米？
（2）若乙挖掘机比甲挖掘每小时多挖掘
米，甲、乙每天挖掘的时间相同，求甲每小时挖掘多少米？
（3）若隧道的总长为
米，甲、乙挖掘机工作
天后，因为甲挖掘机进行设备更新，乙挖掘机设备老化，甲比原来每天多挖
米，同时乙比原来少挖米
．最终，甲、乙两台挖掘机在相同时间里各完成隧道总长的一半，请用含，的代数式表示．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，
，
，点B在x轴上，且
．
求点B的坐标；
求
的面积；
在y轴上是否存在P，使以A、B、P三点为顶点的三角形的面积为10？若存在，请求出点P的坐标；若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在
中，
，点D为AC延长线上一点，连接BD，过A作
，垂足为M，交BC于点N
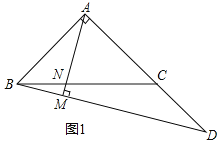
如图1，若
，
，求AM的长；
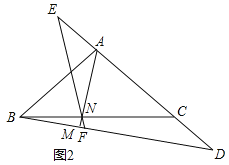
如图2，点E在CA的延长线上，且
，连接EN并延长交BD于点F，求证：
；
在的条件下，当
时，请求出
的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，一次函数y=ax+b的图象与反比例函数
的图象交于C，D两点，与x，y轴交于B，A两点，且tan∠ABO=
，OB=4，OE=2．
（1）求一次函数的解析式和反比例函数的解析式；
（2）求△OCD的面积；
（3）根据图象直接写出一次函数的值大于反比例函数的值时，自变量x的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，∠C＝90°，AB＝5，AC＝4，∠B，∠C的平分线相交于点O，OM∥AB，ON∥AC分别与BC交于点M、N，则△OMN的周长为____．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com