练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    若顺次连接四边形的各边中点所得的四边形是菱形，则该四边形一定是（　　）
    A、矩形
    B、等腰梯形
    C、对角线相等的四边形
    D、对角线互相垂直的四边形
    考点：中点四边形
    专题：
    分析：首先根据题意画出图形，由四边形EFGH是菱形，点E，F，G，H分别是边AD，AB，BC，CD的中点，利用三角形中位线的性质与菱形的性质，即可判定原四边形一定是对角线相等的四边形．
    解答：解：如图，根据题意得：四边形EFGH是菱形，点E，F，G，H分别是边AD，AB，BC，CD的中点，
    ∴EF=FG=CH=EH，BD=2EF，AC=2FG，
    ∴BD=AC．
    ∴原四边形一定是对角线相等的四边形．
    故选：C．
    点评：此题考查了菱形的性质与三角形中位线的性质．此题难度适中，注意掌握数形结合思想的应用．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

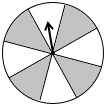    有一个能自由转动的转盘如图，盘面被分成8个大小与性状都相同的扇形，颜色分为黑白两种，将指针的位置固定，让转盘自由转动，当它停止后，指针指向白色扇形的概率是
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    要使分式
    1
    x-10
    有意义，则x的取值范围是
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，在Rt△ABC中，M、N是两直角边上的点，且AM=BC，CM=BN，BM、AN交于点P，则∠APM的度数为
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，在平面直角坐标系xOy中，已知点A（3，4），将OA绕坐标原点O逆时针旋转90°至OA′，则点A′的坐标是
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    反比例函数y=-
    2
    x
    （x＞0），点B为其上一点，点A为x轴负半轴上一点，当点B的横坐标逐渐减小时，△AOB的面积（　　）
    A、逐渐减少B、逐渐增大
    C、不变D、先增大后减小

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，在平面直角坐标系中，点A，B的坐标分别为（-3，0），（0，6）．动点P从点O出发，沿x轴正方向以每秒1个单位的速度运动，同时动点C从点B出发，沿射线BO方向以每秒2个单位的速度运动，以CP，CO为邻边构造?PCOD，在线段OP延长线上取点E，使PE=AO，设点P运动的时间为t秒．
    （1）当点C运动到线段OB的中点时，求t的值及点E的坐标；
    （2）当点C在线段OB上时，求证：四边形ADEC为平行四边形；
    （3）在线段PE上取点F，使PF=1，过点F作MN⊥PE，截取FM=2，FN=1，且点M，N分别在一，四象限，在运动过程中，设?PCOD的面积为S．
    ①当点M，N中有一点落在四边形ADEC的边上时，求出所有满足条件的t的值；
    ②若点M，N中恰好只有一个点落在四边形ADEC的内部（不包括边界）时，直接写出S的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，四边形ABCD为平行四边形，AE⊥BD于E，CF⊥BD于F，垂足分别为E、F．
    （1）求证：BF=DE；
    （2）连接CE、AF，证明四边形CEAF是平行四边形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    先化简，再求值：
    a-3
    3a2-6a
    ÷（a+2-
    5
    a-2
    ），其中a2+3a-1=0．

    查看答案和解析>>

    同步练习册答案