
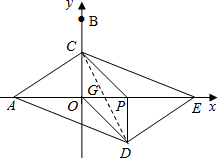
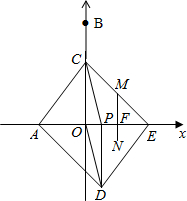
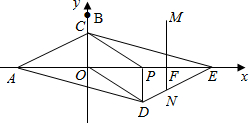
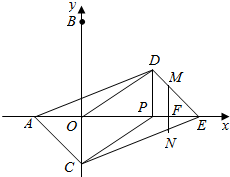
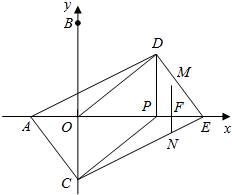
 秒1个单位的速度运动,同时动点C从点B出发,沿射线BO方向以每秒2个单位的速度运动,以CP,CO为邻边构造?PCOD,在线段OP延长线上取点E,使PE=AO,设点P运动的时间为t秒.
秒1个单位的速度运动,同时动点C从点B出发,沿射线BO方向以每秒2个单位的速度运动,以CP,CO为邻边构造?PCOD,在线段OP延长线上取点E,使PE=AO,设点P运动的时间为t秒.| 9 |
| 4 |
| 9 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 9 |
| 2 |
| 9 |
| 2 |
| MF |
| CO |
| EF |
| EO |
| 2 |
| 6-2t |
| 2 |
| 3+t |
| FN |
| PD |
| EF |
| EP |
| 1 |
| 6-2t |
| 2 |
| 3 |
| 9 |
| 4 |
| MF |
| DP |
| EF |
| EP |
| 2 |
| 2t-6 |
| 2 |
| 3 |
| 9 |
| 2 |
| FN |
| OC |
| EF |
| EO |
| 1 |
| 2t-6 |
| 2 |
| 3+t |
| 27 |
| 8 |
| 9 |
| 2 |
| 27 |
| 2 |
| 9 |
| 4 |
| 3 |
| 2 |
| 9 |
| 2 |
| 3 |
| 2 |
| 9 |
| 4 |
| 27 |
| 8 |
| 9 |
| 2 |
| 9 |
| 2 |
| 3 |
| 2 |
| 9 |
| 2 |
| 27 |
| 2 |


科目:初中数学 来源: 题型:
| 1 |
| 22 |
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 4 |
| 1 |
| 22 |
| 1 |
| 32 |
| 1 |
| 2 |
| 3 |
| 2 |
| 2 |
| 3 |
| 4 |
| 3 |
| 1 |
| 2 |
| 4 |
| 3 |
| 2 |
| 3 |
| 1 |
| 22 |
| 1 |
| 32 |
| 1 |
| 42 |
| 1 |
| 2 |
| 3 |
| 2 |
| 2 |
| 3 |
| 4 |
| 3 |
| 3 |
| 4 |
| 5 |
| 4 |
| 1 |
| 2 |
| 5 |
| 4 |
| 5 |
| 8 |
| 1 |
| 22 |
| 1 |
| 32 |
| 1 |
| 42 |
| 1 |
| 52 |
| 1 |
| 2 |
| 3 |
| 2 |
| 2 |
| 3 |
| 4 |
| 3 |
| 3 |
| 4 |
| 5 |
| 4 |
| 4 |
| 5 |
| 6 |
| 5 |
| 1 |
| 2 |
| 6 |
| 5 |
| 3 |
| 5 |
| 1 |
| 22 |
| 1 |
| 32 |
| 1 |
| 42 |
| 1 |
| 52 |
| 1 |
| n2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
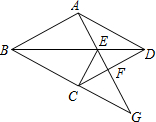 如图,四边形ABCD为菱形,点G为BC的延长线上一点,连接AG,分别交BD、DC于点E、F,连CE.
如图,四边形ABCD为菱形,点G为BC的延长线上一点,连接AG,分别交BD、DC于点E、F,连CE.| FG |
| EF |
| FG |
| EF |
查看答案和解析>>
科目:初中数学 来源: 题型:
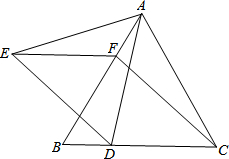 如图,等边△ABC中,D、F分别是边BC、AB上的点,且CD=BF,以AD为边向左作等边△ADE,连接CF、EF,设BD:DC=K.
如图,等边△ABC中,D、F分别是边BC、AB上的点,且CD=BF,以AD为边向左作等边△ADE,连接CF、EF,设BD:DC=K.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,AB为⊙O的直径,以AB为直角边作Rt△ABC,∠CAB=90°,斜边BC与⊙O交于点D,过点D作⊙O的切线DE交AC于点E,DG⊥AB于点F,交⊙O于点G.
如图,AB为⊙O的直径,以AB为直角边作Rt△ABC,∠CAB=90°,斜边BC与⊙O交于点D,过点D作⊙O的切线DE交AC于点E,DG⊥AB于点F,交⊙O于点G.| 2 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
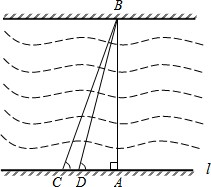 “中国-益阳”网上消息,益阳市为了改善市区交通状况,计划在康富路的北端修建通往资江北岸的新大桥.如图,新大桥的两端位于A、B两点,小张为了测量A、B之间的河宽,在垂直于新大桥AB的直线型道路l上测得如下数据:∠BDA=76.1°,∠BCA=68.2°,CD=82米.求AB的长(精确到0.1米).
“中国-益阳”网上消息,益阳市为了改善市区交通状况,计划在康富路的北端修建通往资江北岸的新大桥.如图,新大桥的两端位于A、B两点,小张为了测量A、B之间的河宽,在垂直于新大桥AB的直线型道路l上测得如下数据:∠BDA=76.1°,∠BCA=68.2°,CD=82米.求AB的长(精确到0.1米).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com