练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    7．如图，在△ABC中，∠A=75°，直线DE分别与边AB，AC交于D，E两点，则∠1+∠2=255°．

    分析 根据三角形的内角和定理结合∠A的度数，即可得出∠ADE+∠AED的度数，再由∠ADE与∠1互补、∠AED与∠2互补，代入数据即可得出结论．

    解答 解：∵∠A=75°，
    ∴∠ADE+∠AED=180°-∠A=105°，
    又∵∠1=180°-∠ADE，∠2=180°-∠AED，
    ∴∠1+∠2=360°-（∠ADE+∠AED）=255°．
    故答案为：255°．

    点评 本题考查了三角形内角和定理，根据三角形内角和定理找出∠ADE+∠AED=105°是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2016-2017学年江苏省无锡市八年级3月月考数学试卷（解析版） 题型：填空题

    如图，DE为△ABC的中位线，点F在DE上，且∠AFB=90?,若AB=5，BC=8，则EF的长为__________．

    查看答案和解析>>

    科目：初中数学 来源：2017届江苏省九年级下学期第一次月考数学试卷（解析版） 题型：单选题

    函数y＝中自变量x的取值范围是(    )

    A. x＞2 B. x≥2 C. x≤2 D. x≠2

    查看答案和解析>>

    科目：初中数学 来源：2016-2017学年江苏省东台市第四教育联盟八年级下学期第一次月考数学试卷（解析版） 题型：填空题

    若使分式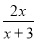有意义，则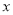的取值范围是____________.

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

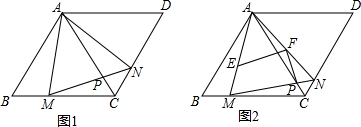    2．如图1，在边长为4的菱形ABCD中，AC为其对角线，∠ABC=60°点M、N分别是边BC、边CD上的动点，且MB=NC．连接AM、AN、MN．MN交AC于点P．
    （1）△AMN是什么特殊的三角形？说明理由．并求其面积最小值；
    （2）求点P到直线CD距离的最大值；
    （3）如图2，已知MB=NC=1，点E、F分别是边AM、边AN上的动点，连接EF、PF，EF+PF是否存在最小值？若存在，求出最小值及此时AE、AF的长；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

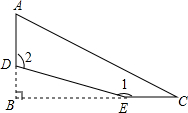    12．有一张直角三角形纸片，记作△ABC，其中∠B=90°．按如图方式剪去它的一个角（虚线部分），在剩下的四边形ADEC中，若∠1=165°，则∠2的度数为105°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．在正方形ABCD中，BD是对角线，点P在射线CD上（与点C、D不重合），连接AP，平移△ADP，使点D移动到点C，得到△BCQ，过点Q作QH⊥BD于点H，连接AH，PH．
    （1）若点P在线段CD上，请按题意补全图；
    （2）AH与PH的数量关系是相等； AH与PH的位置关系是垂直；
    对以上所填的两个结论均加以证明（若需要的话请另外画图）

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

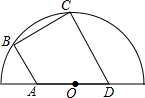    16．如图，四边形ABCD内接于半圆O，其中点A，D在直径上，点B，C在半圆弧上，AB∥CD，∠B=90°，若AO=3，∠BAD=120°，则BC=3$\sqrt{3}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

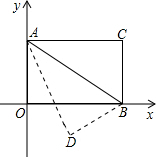    17．已知：如图，长方形AOBC，以O为坐标原点，OB、OA分别在x轴、y轴上，点A坐标为（0，6），∠OAB=60°，以AB为轴对折后，使C点落在D点处，则D点坐标（3$\sqrt{3}$，-3）．

    查看答案和解析>>

    同步练习册答案