
如图,⊙
O的直径AB=12,AM和BN是它的两条切线,切点分别为A、B,DE切⊙O于点E,交AM于点D,交BN于点C.设AD=x,BC=y,则y与x的函数关系式是________.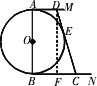
|
答案: y=解法一:如题图,由切线长定理可知, DA=DE,CB=CE,所以CD=DE+CE=AD+BC=x+y.过点D作DF⊥BC,垂足为F,则易知DF=AB=12,BF=AD.所以 CF=BC-BF=BC-AD=y-x.在 Rt△CDF中,由勾股定理,得CD2=DF2+CF2. 所以 (x+y)2=122+(y-x)2.化简,得y=解法二:如图,连接 OD、OC、OE.
由切线长定理可知, AD=DE=x,CB=CE=y,DO平分∠ADC,CO平分∠DCB.因为 AM⊥AB,BN⊥AB,所以 AM∥BC.所以∠ADC+∠DCB=180°.所以∠ ODC+∠DCO=90°,即∠DOC=90°.又因为 DE切⊙O于点E,所以OE⊥CD.从而可得△ ODE∽△COE.所以 |


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
 已知:如图,⊙O的直径AB与弦CD相交于E,
已知:如图,⊙O的直径AB与弦CD相交于E, |
| BC |
 |
| BD |
| 3 |
| 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,⊙O的直径AB与弦CD(不是直径)相交于E,E是CD的中点,过点B作BF∥CD交AD的延长线于
如图,⊙O的直径AB与弦CD(不是直径)相交于E,E是CD的中点,过点B作BF∥CD交AD的延长线于查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,⊙O的直径AB,CD互相垂直,P为 上任意一点,连PC,PA,PD,PB,下列结论:
如图,⊙O的直径AB,CD互相垂直,P为 上任意一点,连PC,PA,PD,PB,下列结论:| CP+DP |
| BP+AP |
| AP |
| DP |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•柳州)如图,⊙O的直径AB=6,AD、BC是⊙O的两条切线,AD=2,BC=
(2013•柳州)如图,⊙O的直径AB=6,AD、BC是⊙O的两条切线,AD=2,BC=| 9 | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com