已知S=12-22+32-42+…+20052-20062+20072,则S除以2005的余数是________.
3
分析:由已知S=1
2-2
2+3
2-4
2+…+2005
2-2006
2+2007
2,可以得出S=-(2
2-1
2)-(4
2-3
2)-(6
2-5
2)-(8
2-7
2)-…-(2006
2-2005
2)+2007
2,?S=-(3+7+11+15+…+4011)+2007
2,不难发现3,7,11,15…4011,是公差为4的等差数列其中4011为1003项,即而求出S.
解答:S=-(2
2-1
2)-(4
2-3
2)-(6
2-5
2)-(8
2-7
2)-…-(2006
2-2005
2)+2007
2=-(3+7+11+15+…+4011)+2007
2=-(3+4011)×1003/2+2007
2=-2007×1003+2007
2=2007×1004.那么S/2005=
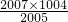
=
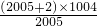
=
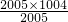
+

故:S除以2005的余数是3.
点评:此题考查了学生分析、归纳发现规律专题的解题能力,采用试求方法得出一等差数列,也是关键.

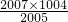 =
=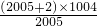 =
=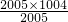 +
+


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案